
【题目】在四边形ABCD中,BC=CD,连接AC、BD,∠ADB=90°.
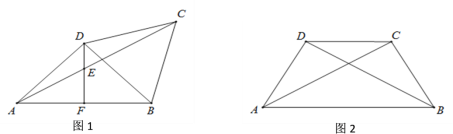
(1)如图1,若AD=BD=BC,过点D作DF⊥AB于点F,交AC于点E:
①∠DAC= °;
②求证:EC=EA+ED;
(2)如图2,若AC=BD,求∠DAC的度数.
【答案】(1)①15°;②见解析;(2)∠DAC=30°.
【解析】
(1)①证明DA=DC,∠ADC=150°,即可求得;②结论:EC=ED+EA.如图1中,设AC交BD于点O,连接BE,在EC上截取EH=EB,由△EBD≌△HBC(SAS),推出DE=CH,可得EC=EH+CH=EB+ED=EA+ED解决问题;
(2)如图2中,作CK⊥BD于K,CH⊥AD交AD的延长线于H,首先证明四边形DHCK是矩形,再证明CH=AC,即可解决问题;
(1)①如图1中,
∵AD=BD=BC,BC=CD,
∴BD=BC=CD,
∴△BDC是等边三角形,
∴∠CDB=60°,
∵∠ADB=90°,
∴∠ADC=90°+60°=150°,
∵DA=DC,
∴∠DAC=∠DCA=15°;
故答案为:15°;
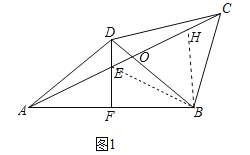
②结论:EC=ED+EA.如图1中,设AC交BD于点O,连接BE,在EC上截取EH=EB.

∵DA=DB,DF⊥AB,
∴AF=FB,
∴EA=EB,
∴∠DAF=∠DBF,∠EAB=∠EBA,
∴∠DAE=∠DBE,
∵∠DAE=∠DCO,
∴∠DCO=∠OBE,
∵∠DOC=∠EOB,
∴∠BEO=∠ODC=60°,
∵EH=EB,
∴△EBH是等边三角形,
∴∠EBH=∠DBC=60°,BE=BH,
∴∠EBD=∠HBC,
∵BD=BC,
∴△EBD≌△HBC(SAS),
∴DE=CH,
∴EC=EH+CH=EB+ED=EA+ED.
(2)如图2中,作CK⊥BD于K,CH⊥AD交AD的延长线于H.
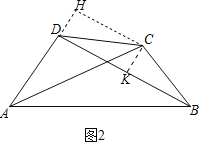
∵∠H=∠CKD=∠HDK=90°,
∴四边形DHCK是矩形,
∴DK=CH,
∵CD=CB.CK⊥BD,
∴DK=![]() BD,
BD,
∵AC=BD,
∴CH=![]() AC,
AC,
在Rt△ACH中,sin∠CAD=![]() ,
,
∴∠CAD=30°.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
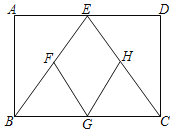
【题目】如图,已知四边形ABCD是矩形,点E,G分别是AD,BC边的中点,连接BE,CE,点F,H分别是BE,CE的中点连接FG,HG.
(1)求证:四边形EFGH是菱形;
(2)当![]() = 时,四边形EFGH是正方形.
= 时,四边形EFGH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
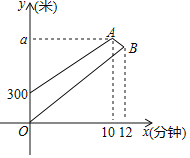
【题目】小明放学后从学校回家,出发![]() 分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发
分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发![]() 分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程
分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程![]() (米)与小强所用时间
(米)与小强所用时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求函数图象中![]() 的值;
的值;
(2)求小强的速度;
(3)求线段![]() 的函数解析式,并写出自变量的取值范围.
的函数解析式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,将
上,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,且
处,且![]() .
.
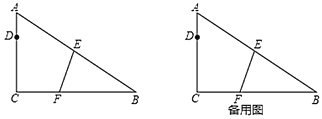
(1)求![]() 的长;
的长;
(2)点![]() 是射线
是射线![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积与
的面积与![]() 的面积相等,
的面积相等,
①当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ________;
________;
(3)将直线![]() 平移,平移后的直线与直线
平移,平移后的直线与直线![]() ,直线
,直线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,以线段
,以线段![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧,连接
两侧,连接![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
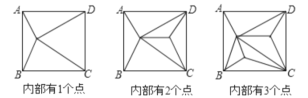
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
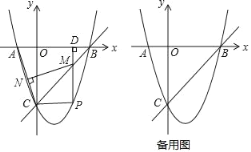
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=x﹣3经过B,C两点.
(1)求抛物线的解析式;
(2)点P是第四象限内抛物线上的动点,过点P作PD⊥x轴于点D,交直线BC于点M,连接AC,过点M作MN⊥AC于点N,设点P的横坐标为t.
①求线段MN的长d与t之间的函数关系式(不要求写出自变量t的取值范围);
②点Q是平面内一点,是否存在一点P,使以B,C,P,Q为顶点的四边形为矩形?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF的边长为2,现将它沿AB方向平移1个单位,得到正六边形A′B′C′D′E′F′,则阴影部分A′BCDE′F′的面积是( )
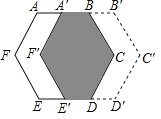
A.3![]() B.4
B.4![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com