
【题目】按要求解方程:
①y(y﹣2)=3 y2﹣1(公式法)
②x2+8x+9=0(配方法)
③(2x﹣1)2﹣3(2x﹣1)+2=0(因式分解法)
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
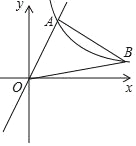
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
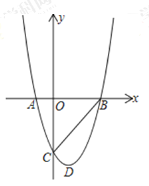
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其顶点
,其顶点![]() 的坐标为
的坐标为![]() 为抛物线上
为抛物线上![]() 轴下方一点.
轴下方一点.
(1)求抛物线的解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若直线![]() 与抛物线交于
与抛物线交于![]() 两点,问:是否存在
两点,问:是否存在![]() 的值,使得
的值,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
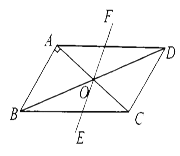
【题目】如图,□ABCD中,AB⊥AC,AB=1,BC=![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)试说明在旋转过程中,线段AF与EC总保持相等;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,请直接写出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
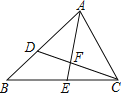
【题目】如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
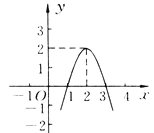
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com