
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其顶点
,其顶点![]() 的坐标为
的坐标为![]() 为抛物线上
为抛物线上![]() 轴下方一点.
轴下方一点.
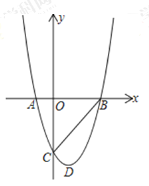
(1)求抛物线的解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若直线![]() 与抛物线交于
与抛物线交于![]() 两点,问:是否存在
两点,问:是否存在![]() 的值,使得
的值,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)由于已知抛物线顶点坐标,故可设顶点式,再把点B坐标代入求得a,即求得抛物线解析式;
(2)先根据抛物线解析式求出A、C坐标.由∠PCB=∠ACB和∠ABC=45°联想到构造△ABC的全等三角形,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,构造角边角得到的△ABC≌△MBC,进而求得点M坐标.求直线CM解析式,把直线CM与抛物线解析式联立方程组,求得的其中一解即为点P坐标;
,构造角边角得到的△ABC≌△MBC,进而求得点M坐标.求直线CM解析式,把直线CM与抛物线解析式联立方程组,求得的其中一解即为点P坐标;
(3)假设存在![]() 的值,使直线
的值,使直线![]() 与(1)中所求的抛物线
与(1)中所求的抛物线![]() 交于
交于![]() 、
、![]() ,联立两函数解析式求出
,联立两函数解析式求出![]() ,根据OM2+ON2=MN2,整理后把x1+x2和x1·x2的值代入即可求出a的值.
,根据OM2+ON2=MN2,整理后把x1+x2和x1·x2的值代入即可求出a的值.
(1)设抛物线解析式为y=a(x-1)2-4,把B(3,0)代入得,
![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,
,
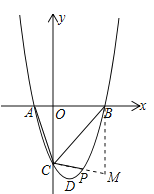
∵y=0时,x2-2x-3=0,
解得:x1=-1,x2=3,
∴A(-1,0),AB=3-(-1)=4,
∵x=0时,y=x2-2x-3=-3,
∴C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°.
∵OC∥BM,
∴∠MBC=∠OCB=∠OBC=45°,
在△ABC与△MBC中,
 ,
,
∴△ABC≌△MBC(ASA)
![]() ,
,
![]() ,
,
设CM解析式为y=kx+b,
把C(0,-3),![]() 代入,得
代入,得
![]() ,
,
∴ ,
,
![]() ,
,
由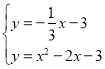 ,得
,得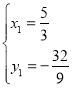 或
或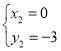 (舍),
(舍),
![]() ;
;
(3)假设存在![]() 的值,使直线
的值,使直线![]() 与(1)中所求的抛物线
与(1)中所求的抛物线![]() 交于
交于![]() 、
、![]() ,
,
两点(![]() 在
在![]() 的左侧),使得
的左侧),使得![]() ,
,
由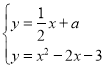 得
得![]() ,
,
![]() ,
,
又![]() ,
,
![]()
![]() ,
,
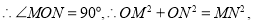
![]() ,
,
![]() ,
,
![]() 即
即![]() ,
,
![]() ,
,
![]() 存在
存在![]() 使得
使得![]() .
.


科目:初中数学 来源: 题型:
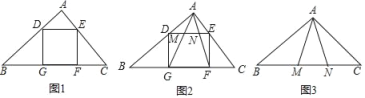
【题目】(1)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,若AB=AC=2,求DE的长;
(2)如图,在(1)的条件下,连结AG、AF分别交DE于M、N两点,求MN的长;
(3)如图,在△ABC中,AB=AC=BN=2,∠BAC=108°,若AM=AN,请直接写出MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
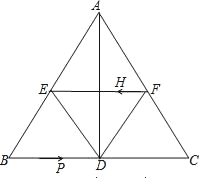
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
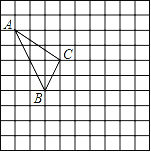
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
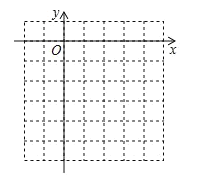
(1)画出该二次函数的图象;
(2)连接AC、CD、BD,求ABCD的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
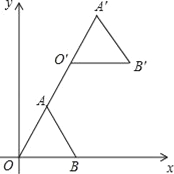
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形。把它们沿图中虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为多少cm![]() ( )
( )
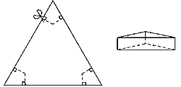
A. 124B. 144C. 110D. 94
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com