
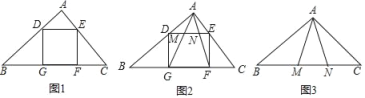
【题目】(1)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,若AB=AC=2,求DE的长;
(2)如图,在(1)的条件下,连结AG、AF分别交DE于M、N两点,求MN的长;
(3)如图,在△ABC中,AB=AC=BN=2,∠BAC=108°,若AM=AN,请直接写出MN的长.
【答案】(1)DE=![]() ;(2)MN=
;(2)MN=![]() ;(3)MN=3﹣
;(3)MN=3﹣![]() .
.
【解析】
(1)先利用勾股定理求出BC的长,然后证明△BGD和△EFC是等腰直角三角形,根据正方形的性质可得BG=FG=FC即可解决问题.
(2)利用平行线分线段成比例定理,构建方程即可解决问题.
(3)证明BM=AM=AN,设MN=x,则AN=AM=BM=2-x.由△NAM∽△NBA,可得AN2=NMNB,构建方程即可解决问题.
(1)解:∵AB=AC=2,∠A=90°,
∴∠B=∠C=45°,BC=![]() ,
,
∵四边形DEFG是正方形,
∴DE=DG=GF=EF,∠DGF=∠EFG=90°,
∴∠BGD=∠CFE=90°,
∴∠B=∠BDG=45°,∠C=∠CEF=45°,
∴BG=DG, CF=EF,
∴BG=FG=FC=DE,
∴DE=![]() BC=
BC=![]() .
.
(2)∵DE∥BC,
∴![]() ,
,
∴![]() ,
,
∴MN=![]() .
.
(3)∵AB=AC,∠BAC=108°,
∴∠B=∠C=36°,
∵BA=NB,
∴∠ANB=∠BAN=72°,
∵AM=AN,
∴∠AMN=∠ANM=72°,
∴∠B=∠BAM=∠MAN=36°,
∴BM=AM=AN,设MN=x,则AN=AM=BM=2﹣x.
∵△NAM∽△NBA,
∴AN2=NMNB,
∴(2﹣x)2=2x,
∴x=3﹣![]() 或3+
或3+![]() (舍弃)
(舍弃)
∴MN=3﹣![]() .
.


科目:初中数学 来源: 题型:
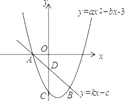
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
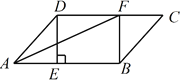
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳跳一家外出自驾游,出发时油箱里还剩有汽油30升,已知跳跳家的汽车每百千米的平均油耗为12升,设油箱里剩下的油量为y(单位:升),汽车行驶的路程为x(单位:千米).
(1)求y关于x的函数表达式;
(2)若跳跳家的汽车油箱中的油量低于5升时,仪表盘会亮起黄灯警报. 要使邮箱中的存油量不低于5升,跳跳爸爸至多能够行驶多少千米就要进加油站加油?
查看答案和解析>>
科目:初中数学 来源: 题型:
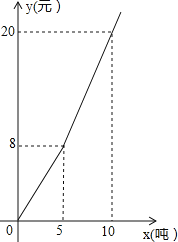
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球,记下数字为x,且不放回盒子,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小米、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店准备销售一种多功能旅行背包,计划从厂家以每个120元的价格进货.

(1)经过市场调查发现,当每个背包的售价为140元时,月均销量为980个,售价每增长10元,月均销量就相应减少30个,若使这种背包的月均销量不低于800个,每个背包售价应不高于多少元?
(2)在实际销售过程中,由于原材料涨价和生产成本增加的原因,每个背包的进价为150元,而每个背包的售价比(1)中最高售价减少了a%(a>0),月均销量比(1)中最低月均销量800个增加了5a%,结果该店销售该背包的月均利润达到了40000元,求在实际销售过程中每个背包售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
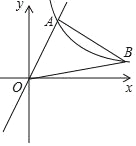
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
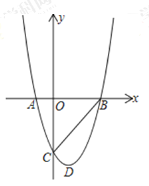
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其顶点
,其顶点![]() 的坐标为
的坐标为![]() 为抛物线上
为抛物线上![]() 轴下方一点.
轴下方一点.
(1)求抛物线的解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若直线![]() 与抛物线交于
与抛物线交于![]() 两点,问:是否存在
两点,问:是否存在![]() 的值,使得
的值,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com