
【题目】如图,正方形ABCD中点E为AD的中点,连接CE,将△CDE绕点C逆时针旋转得△CGF,点G在CE上,作DM⊥CE于点M,连接BM交CF于N,已知四边形GFNM面积为27,则正方形ABCD的边长为_________.
【答案】10![]()
【解析】
作BH⊥EC于H,可证△BCH≌△DMC,可得DM=CH,根据锐角三角函数可得CM=2DM,则H是CM中点,可得∠BMC=∠BCM,再证△MNC∽△FGC,根据面积比等于相似比的平方,可求正方形ABCD的边长
作BH⊥EC于H
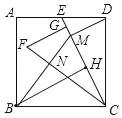
设BC=CD=AD=2a,
∵E为AD中点,
∴DE=a,
∴S△DEC=a2.
根据勾股定理得EC=![]() a,
a,
∵∠HBC+∠HCB=90°,∠ECD+∠HCB=90°,
∴∠ECD=∠HBC,且CD=BC,∠BHC=∠DMC=90°,
∴△DMC≌△BHC,
∴CH=MD,BH=CM,
∵sin∠DCE=![]() ,
,
∴![]() ,
,
∴DM=![]() a,
a,
∴CM=![]() =
=![]() a,
a,
∴CH=![]() a,
a,
∴MH=CH,且BH⊥CM,
∴BM=BC,
∴∠BMC=∠BCM,
∵AD∥BC,
∴∠DEC=∠ECB,
∵旋转
∴∠F=∠DEC,CF=CE=![]() a
a
∴∠F=∠BMC,∠MCF=∠MCF
∴△MNC∽△GFC
∴![]() ,
,
![]() ,
,
∴S△MNC=![]() ,
,
∴SFGMN=a2﹣![]() =
=![]() ,
,
∴![]() =27,
=27,
∴a=5![]() ,
,
∴2a=10![]() ,
,
故答案为:10![]()


科目:初中数学 来源: 题型:
【题目】如图所示的转盘,分成三个相同的扇形,指针位置固定转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,当作指向右边的扇形).
(1)求事件“转动一次,得到的数恰好是0”发生的概率;
(2)写出此情景下一个不可能发生的事件.
(3)用树状图或列表法,求事件“转动两次,第一次得到的数与第二次得到的数绝对值相等”发生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC.其中正确的有( )个.
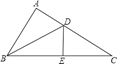
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
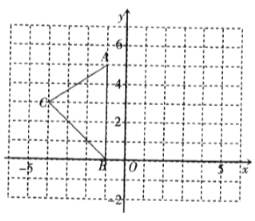
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,们一个图形都是由一些黑点按一定的规律排列组成的,其中第①个图形中共有6个小黑点,第②个图形中有10个黑点,第③个图形中一共有16个小黑点,…,按此规律,则第⑩个图形中小黑点的个数是( )

A. 112 B. 114 C. 116 D. 118
查看答案和解析>>
科目:初中数学 来源: 题型:
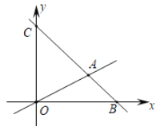
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)直线![]() 的关系式为 ;直线
的关系式为 ;直线![]() 的关系式为 (直接写出答案,不必写过程).
的关系式为 (直接写出答案,不必写过程).
(2)求![]() 的面积.
的面积.
(3)若有一动点![]() 沿路线
沿路线![]() 运动,当
运动,当![]() 时,求点
时,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中A(3,2),B(4,3),C(1,1).
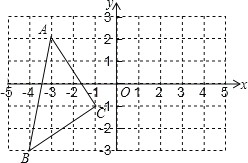
(1)在图中作出△ABC关于y轴对称图形△A1B1C1;
(2)写出A1、B1、C1的坐标分别是A1(___,___),B1(___,___),C1(___,___);
(3)△ABC的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com