某商店把一商品按标价的九折出售（即优惠10%），仍可获利20%，若该商品的标价为每件28元，则该商品的进价为（ ）
A．21元 B．19.8元 C．22.4元 D．25.2元
心算口算巧算一课一练系列答案科目：初中数学 来源： 题型：
为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看3次的人数没有标出）．
根据上述信息，解答下列问题：
（1）该班级女生人数是 ，女生收看“两会”新闻次数的中位数是 ；
（2）对于某个群体，我们把一周内收看热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体多某热点新闻的“关注指数”，如果该班级男生对“两会”新闻的“关注指数”比女生低5%，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量，根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小．
| 统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
| 该班级男生 | 3 | 3 | 4 | 2 | … |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图（1），边长为4的正方形ABCD中，点E在AB边上（不与点A、B重合），
点F在BC边上（不与B、C）重合.
第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G;
第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时记为点H;
依次操作下去……
（1）图（2）中的△DEF是经过两次操作后得到的，其形状为 ，求此时
线段EF的长；
（2）若经过三次操作可得到四边形EFGH，
①请判断四边形EFGH的形状为 ，此时AE与BF的数量关系是 ；
②以①中的结论与前提，设AE的长为x，四边形EFGH的面积
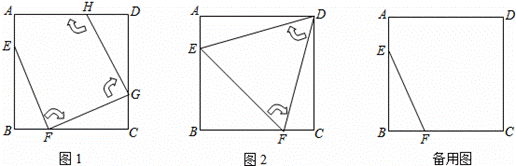求y与x的函数关系式及面积y的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
今年哥哥的年龄是妹妹年龄的2倍，4年前哥哥的年龄是妹妹年龄的3倍，若设妹妹今年x岁，可列方程为（ ）
A．2x﹣4=3（x﹣4） B．2x=3（x﹣4） C．2x+4=3（x﹣4） D．2x+4=3x
查看答案和解析>>
科目：初中数学 来源： 题型：
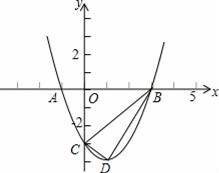
如图，已知抛物线y=ax2+bx﹣3与x轴的一个交点为A（﹣1，0），另一个交点为B，与y轴的交点为C，其顶点为D，对称轴为直线x=1．
（1）求抛物线的解析式；
（2）已知点M为y轴上的一个动点，当△ACM是以AC为一腰的等腰三角形时，求点M的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，相似比为1:2，则△ABC与
CE，求线段CE的长．