
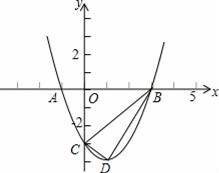
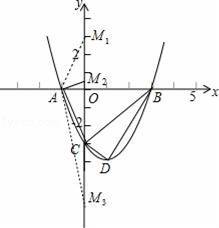
如图,已知抛物线y=ax2+bx﹣3与x轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C,其顶点为D,对称轴为直线x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ACM是以AC为一腰的等腰三角形时,求点M的坐标.

【考点】抛物线与x轴的交点;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.
【专题】计算题.
【分析】(1)利用对称性可得B(3,0),则利用交点式得抛物线解析式为y=a(x+1)(x﹣3)=ax2﹣2ax﹣3a,所以﹣3a=3,解得a=1,于是得到抛物线解析式为y=x2﹣2x﹣3;
(2)分类讨论:当AC=AM时,易得点M1(0,3),如图;②当CM=CA时,先计算出AC=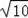
 ,再以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,易得M2(0,
,再以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,易得M2(0,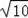
 ﹣1),M3(0,﹣
﹣1),M3(0,﹣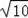
 ﹣3).
﹣3).
【解答】解:(1)∵点A(﹣1,0)和点B关于直线x=1对称,
∴B(3,0),
∴抛物线解析式为y=a(x+1)(x﹣3)=ax2﹣2ax﹣3a,
∴﹣3a=3,解得a=1,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)当AC=AM时,点M1与点C关于x轴对称,则M1(0,3),如图;
②当CM=CA时,AC=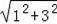
 =
=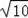
 ,
,
以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,则OM2=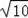
 ﹣1,OM3=OC+CM3=3+
﹣1,OM3=OC+CM3=3+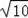
 ,则M2(0,
,则M2(0,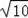
 ﹣1),M3(0,﹣
﹣1),M3(0,﹣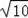
 ﹣3).
﹣3).
综上所述,满足条件的点M的坐标为(0,3),(0,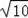
 ﹣1),(0,﹣
﹣1),(0,﹣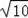
 ﹣3).
﹣3).

【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(2)小题的关键是利用等腰三角形的性质画出点M的坐标.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
某商店把一商品按标价的九折出售(即优惠10%),仍可获利20%,若该商品的标价为每件28元,则该商品的进价为( )
A.21元 B.19.8元 C.22.4元 D.25.2元
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
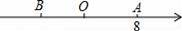

查看答案和解析>>
科目:初中数学 来源: 题型:
在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果,节目组规定:每位选手至少获得两位评委的“通过”才能晋级
(1)请用树形图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
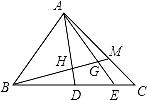
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com