
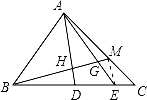
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
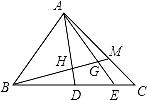
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
D【考点】相似三角形的判定与性质.
【专题】计算题.
【分析】连接EM,根据已知可得△BHD∽△BME,△CEM∽△CDA,根据相似比从而不难得到答案.
【解答】解:连接EM,
CE:CD=CM:CA=1:3
∴EM平行于AD
∴△BHD∽△BME,△CEM∽△CDA
∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3
∴AH =(3﹣
=(3﹣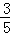 )ME,
)ME,
∴AH:ME=12:5
∴HG:GM=AH:EM=12:5
设GM=5k,GH=12k,
∵BH:HM=3:2=BH:17k
∴BH=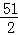 K,
K,
∴BH:HG:GM=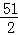 k:12k:5k=51:24:10
k:12k:5k=51:24:10
故选D.
【点评】此题主要考查相似三角形的性质的理解及运用.


科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( )
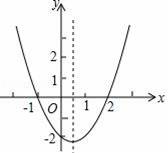

A.函数有最小值 B.当﹣1<x<2时,y>0
C.a+b+c<0 D.当x<
 ,y随x的增大而减小
,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
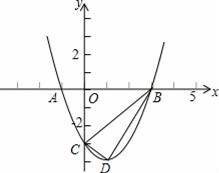
如图,已知抛物线y=ax2+bx﹣3与x轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C,其顶点为D,对称轴为直线x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ACM是以AC为一腰的等腰三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=﹣2x2+1向右平移1个单位,再向下平移3个单位后所得到的抛物线为( )
A.y=﹣2(x+1)2﹣2 B.y=﹣2(x+1)2﹣4 C.y=﹣2(x﹣1)2﹣2 D.y=﹣2(x﹣1)2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
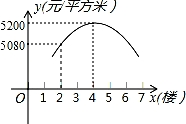
某市新建成的一批楼房都是8层,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化.已知点(x,y)都在一个二次函数的图象上(如图),则6楼房子的价格为 元/平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
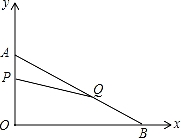
在平面直角坐标系内,已知点A(0,6),点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t=2秒时,求四边形OPQB的面积;
(3)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com