
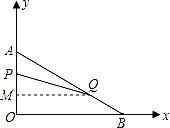
在平面直角坐标系内,已知点A(0,6),点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t=2秒时,求四边形OPQB的面积;
(3)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
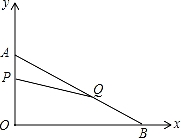
【考点】一次函数综合题.
【分析】(1)根据直线经过点A、B,利用待定系数法求出函数的解析式;
(2)过点Q作QM⊥OA于M,由△AMQ∽△AOB求出QM的值,求出四边形OPQB的面积;
(3)以点A、P、Q为顶点的三角形与△AOB相似,分△APQ∽△AOB和△AQP∽△AOB两种情况讨论,根据相似三角形的对应边的比相等,就可以求出t的值.
【解答】解:(1)设直线AB的解析式为y=kx+b,
将点A(0,6)、点B(8,0)代入得,
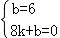 ,
,
解得,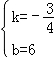 ,
,
∴直线AB的解析式为y=﹣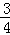 x+6;
x+6;
(2)过点Q作QM⊥OA于M,
当t=2秒时,AP=2,AQ=AB﹣BQ=6,
在Rt△OAB中,OA=6,OB=8,
由勾股定理可得,AB=10,
∵∠AOB=90°,QM⊥OA,
∴△AMQ∽△AOB,
∴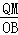 =
=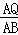 ,即
,即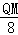 =
=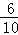 ,
,
解得,QM=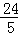 ,
,
∴△APQ的面积=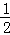 ×AP×QM=
×AP×QM=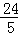 ,
,
∴四边形OPQB的面积=△AOB的面积﹣△APQ的面积=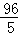 ;
;
(3)由题意得,AO=6,BO=8,AB=10,AP=t,AQ=10﹣2t,
当△APQ∽△AOB时,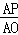 =
=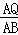 ,即
,即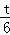 =
=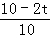 ,
,
解得,t=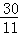 ;
;
当△APQ∽△ABO时,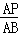 =
=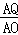 ,即
,即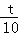 =
=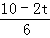 ,
,
解得,t=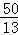 ,
,
因此,t=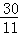 或t=
或t=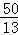 时,以点A.P.Q为顶点的三角形与△AOB相似.
时,以点A.P.Q为顶点的三角形与△AOB相似.
【点评】本题考查的是相似三角形的判定和 性质以及一次函数解析式的确定,掌握相似三角形的判定定理和性质定理、待定系数法求一次函数解析式是解题的关键.
性质以及一次函数解析式的确定,掌握相似三角形的判定定理和性质定理、待定系数法求一次函数解析式是解题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
若a=﹣2×32,b=(﹣2×3)2,c=﹣(2×3)2,则下列大小关系中正确的是( )
A.a>b>c B.b>c>a C.b>a>c D.c>a>b
查看答案和解析>>
科目:初中数学 来源: 题型:
在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果,节目组规定:每位选手至少获得两位评委的“通过”才能晋级
(1)请用树形图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
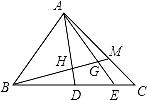
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
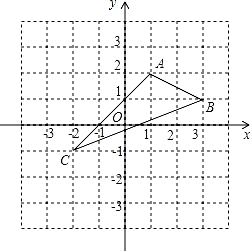
如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.
(2)写出点A1,B1,C1的坐标(直接写答案).
A1
B1
C1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com