

分析 (1)点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,可以求得∠AOC和∠BOC的度数;
(2)根据∠AOC的度数和∠MON的度数可以得到∠CON的度数;
(3)根据∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,可以得到∠BON-∠COM的度数.
解答 解:(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
点评 本题考查角的计算,解题的关键是找出各个角之间的关系,与已知条件建立关系,然后求出所求角的度数.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解一批袋装食品是否含有防腐剂 | |
| B. | 了解某班学生“50米跑”的成绩 | |
| C. | 了解江苏卫士“非诚勿扰”节目的收视率 | |
| D. | 调查我市冷饮市场雪糕质量情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
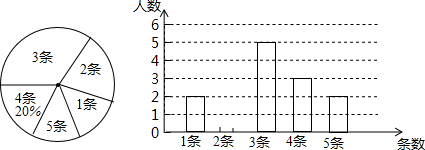
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-4}\\{y=-3}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-39x+180=0 | B. | 2x2+39x+180=0 | C. | 2x2-39x-180=0 | D. | 2x2+39x-180=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com