
| A. | x2-x-1=0 | B. | x2-x+1=0 | C. | x2+x-1=0 | D. | x2-x=0 |
分析 判断上述四个方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了.
解答 解:A、∵△=b2-4ac=1+4=5>0,∴方程有两个不相等的实数根,故本选项错误;
B、∵△=b2-4ac=1-4=-3<0,∴方程没有实数根,故本选项正确;
C、∵△=b2-4ac=1+4=5>0,∴方程有两个不相等的实数根,故本选项错误;
D、∵△=b2-4ac=1-0=1>0,∴方程有两个不相等的实数根,故本选项错误;
故选B.
点评 此题考查了根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
 如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=-1.
如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
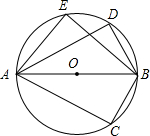 如图,已知AB是⊙O的直径,C,D,E是⊙O上的三个点,在下列各组角中,相等的是( )
如图,已知AB是⊙O的直径,C,D,E是⊙O上的三个点,在下列各组角中,相等的是( )| A. | ∠C和∠D | B. | ∠DAB和∠CAB | C. | ∠C和∠EBA | D. | ∠DAB和∠DBE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
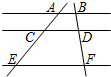 如图,如果AB∥CD∥EF,那么下列结论正确的是( )
如图,如果AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AC}{AE}$=$\frac{CD}{EF}$ | B. | $\frac{AC}{BD}$=$\frac{CE}{DF}$ | C. | $\frac{AC}{CE}$=$\frac{AB}{CD}$ | D. | $\frac{AC}{DF}$=$\frac{BD}{CE}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com