
【题目】如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为 . 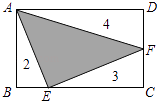
 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)2﹣1+![]()
(2)2x2y(﹣3xy)÷(xy)2
(3)(﹣2a)(3a2﹣a+3)
(4)(x+3)(x+4)﹣(x﹣1)2
(5)[2a3x2(a﹣2x)﹣![]() a2x2]÷(﹣ax)2
a2x2]÷(﹣ax)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.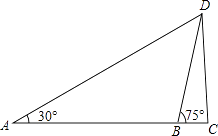
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )

A.△ABC中,AB边上的高是CEB.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CED.△ACD中,CD边上的高是AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,BD是△ABC的角平分线,点D在AC上,DE∥BC,交AB于点E,∠A=50°,∠ADB=110°,求△BDE各内角的度数;


(2)完成下列推理过程.
已知:如图2,AD⊥BC,EF⊥BC,∠1=∠2,求证:DG∥AB.推理过程:因为AD⊥BC,EF⊥BC(已知),
所以∠EFB=∠ADB=90°(________).
所以EF∥AD(同位角相等,两直线平行).
所以∠1=∠BAD(________).
因为∠1=∠2(已知),
所以________=________(等量代换).
所以DG∥AB(内错角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
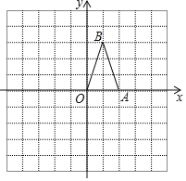
【题目】如图,在平面直角坐标系中,已知点A(2,0),点B(1,3).
(1)画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)画出△OAB关于原点O的中心对称图形△OA2B2,并写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比学习)
小明同学类比除法2401615的竖式计算,想到对二次三项式x23x2进行因式分解的方法:


即x23x2x1x2,所以x23x2x1x2.
(初步应用)
小明看到了这样一道被墨水污染的因式分解题:x2□x6x2x☆,(其中□、☆代表两个被污染的系数),他列出了下列竖式:

得出□=___________,☆=_________.
(深入研究)
小明用这种方法对多项式x22x2-x-2进行因式分解,进行到了:x32x2-x-2x2*.(*代表一个多项式),请你利用前面的方法,列出竖式,将多项式x32x2-x-2因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
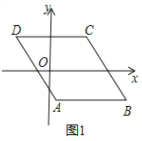
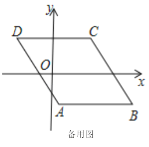
【题目】如图1,已知ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是ABCD边上的一个动点.
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从![]() 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com