
【题目】如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.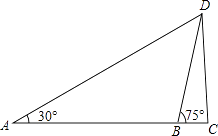
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
【答案】
(1)解:过点B作BE⊥AD于点E,
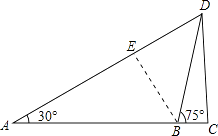
∵AB=40m,∠A=30°,
∴BE= ![]() AB=20m,AE=
AB=20m,AE= ![]() =20
=20 ![]() m,
m,
即点B到AD的距离为20m
(2)解:在Rt△ABE中,
∵∠A=30°,
∴∠ABE=60°,
∵∠DBC=75°,
∴∠EBD=180°﹣60°﹣75°=45°,
∴DE=EB=20m,
则AD=AE+EB=20 ![]() +20=20(
+20=20( ![]() +1)(m),
+1)(m),
在Rt△ADC中,∠A=30°,
∴DC= ![]() =(10+10
=(10+10 ![]() )m.
)m.
答:塔高CD为(10+10 ![]() )m.
)m.
【解析】(1)通过作垂线,把30度角放在直角三角形中, 利用30度角的性质可求得 B到AD的距离 ;(2) 利用外角定理可∠EBD=45°,DE=EB=20m则AD=AE+EB,在Rt△ADC中,∠A=30°,DC=![]() A D ,求出CD.
A D ,求出CD.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】(1)发现问题:如图①平行四边形AB、CD的对角线相交于点O,DE∥AC,CE∥BD,可知:四边形OCED是什么形(不需要证明).
(2)类比探究:如图②矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,四边形OCED是什么形,请说明理由;
(3)拓展应用:如图③,菱形ABCD的对角线相交于点O,∠ABC=60°,BC=4,DE∥AC交BC的延长线于点F,CE∥BD求四边形ABFD的周长.
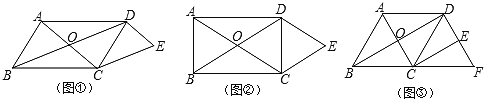
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
(1)求证:△AED≌△CFB;
(2)求证:四边形AFCE是平行四边形
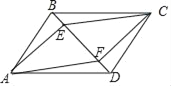
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.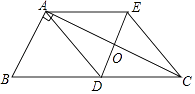
(1)求证:四边形ADCE是菱形;
(2)作出△ABC外接圆,不写作法,请指出圆心与半径;
(3)若AO:BD= ![]() :2,求证:点E在△ABC的外接圆上.
:2,求证:点E在△ABC的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
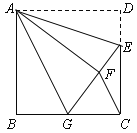
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
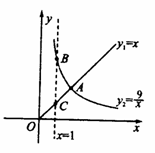
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像经过点
的图像经过点![]() .
.
(1)求k的值,并判断点![]() 是否在该反比例函数的图像上;
是否在该反比例函数的图像上;
(2)该反比例函数图像在第______象限,在每个象限内,y随x的增大而_______.
(3)当![]() 时,求y的取值范围.
时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=30°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=84°,则∠![]() EA度数为( )
EA度数为( )
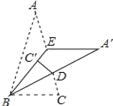
A.54°B.81°C.108°D.114°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com