
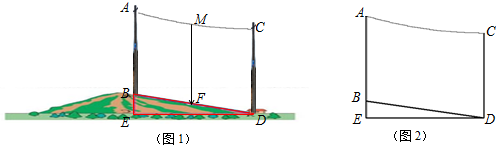
分析 以点A为原点,建立坐标系,由在一个坡度i=1:7的斜坡面BD上,水平距离DE为14米,求得BE=2m,设A点坐标为原点,根据架设两根高度均为10米的电杆DC和BA,求得C(14,-2),设此抛物线解析式为:y=$\frac{1}{98}$x2+bx,把C(14,-2)代入-2=$\frac{1}{98}$×142+b×14,解得b=-$\frac{2}{7}$,于是得到y=$\frac{1}{98}$x2-$\frac{2}{7}$x=$\frac{1}{98}$(x2-28x)=$\frac{1}{98}$(x-14)2-2,设抛物线的顶点为M,则M(14,-2),由C(14,-2),求得M与C重合,过C作CH⊥BD于H,得到△CDH∽△DBE,根据相似三角形的性质即可得到结论.
解答 解:如图,以点A为原点,建立坐标系,
∵在一个坡度i=1:7的斜坡面BD上,水平距离DE为14米,
∴BE:DE=1:7,
∴BE=2m,
设A点坐标为原点,
∵架设两根高度均为10米的电杆DC和BA,
∴C(14,-2),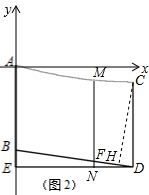
∵A、C两端挂起的电线下垂近似成抛物线y=$\frac{1}{98}$x2形状,
∴设此抛物线解析式为:y=$\frac{1}{98}$x2+bx,
-2=$\frac{1}{98}$×142+b×14,
解得:b=-$\frac{2}{7}$,
∴y=$\frac{1}{98}$x2-$\frac{2}{7}$x=$\frac{1}{98}$(x2-28x)=$\frac{1}{98}$(x-14)2-2,
∴设抛物线的顶点为M,则M(14,-2),∵C(14,-2),
∴M与C重合,
过C作CH⊥BD于H,∴△CDH∽△DBE,
∴$\frac{CH}{DE}=\frac{CD}{DB}$,
∵DB=$\sqrt{{2}^{2}+1{4}^{2}}$=10$\sqrt{2}$,
∴CH=7$\sqrt{2}$,
∴下垂电线与坡面的距离MF的最小值是7$\sqrt{2}$m.
点评 本题主要考查了二次函数在实际生活中的应用,相似三角形的判定和性质,勾股定理,熟练运用二次函数的性质是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:2017届辽宁省大石桥市中考模拟(一)数学试卷(解析版) 题型:单选题
下列运算中,正确的是
A. 2a2+3a2=5a4 B. 5a2-2a2=3
C. a3×2a2=2a6 D. 3a6÷a2=3a4
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
已知:关于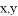 的方程组
的方程组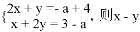 的值为( )
的值为( )
A. -1 B. 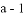 C. 0 D. 1
C. 0 D. 1
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:填空题
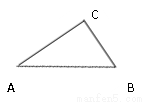
如图,AC⊥BC, 且BC=6,AC=8,AB=10,则点B到AC的距离是 .
A. 6 B. 7 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
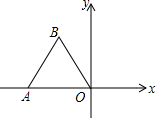 如图,△OAB是边长为2的等边三角形.
如图,△OAB是边长为2的等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com