
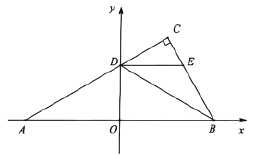
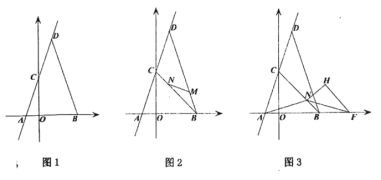
【题目】如图平面直角坐标系中,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() ,点
,点![]() 在
在![]() 轴上方,
轴上方,![]() ,
,![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)点![]() 的坐标为 .
的坐标为 .
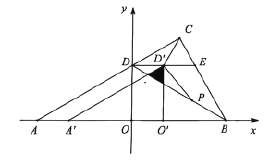
(2)将![]() 沿线段
沿线段![]() 向右平移得
向右平移得![]() ,当点
,当点![]() 与
与![]() 重合时停止运动,记
重合时停止运动,记![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,求
时,求![]() 的最小值;
的最小值;
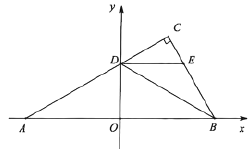
(3)当![]() 移动到点
移动到点![]() 与
与![]() 重合时,将
重合时,将![]() 绕点
绕点![]() 旋转一周,旋转过程中,直线
旋转一周,旋转过程中,直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、点
、点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .当
.当![]() 为直角三角形时,直接写出线段
为直角三角形时,直接写出线段![]() 的长.
的长.
【答案】(1)C(3,3![]() );(2)最小值为2+2
);(2)最小值为2+2![]() ;(3)D0H的值为2
;(3)D0H的值为2![]() -2或2
-2或2![]() +2或4
+2或4![]() -4或4
-4或4![]() +4.
+4.
【解析】
(1)想办法求出A,D,B的坐标,求出直线AC,BC的解析式,构建方程组即可解决问题.
(2)如图2中,设BD交O′D′于G,交A′D′于F.作PH⊥OB于H.利用三角形的面积公式求出点D坐标,再证明PH=![]() PB,把问题转化为垂线段最短即可解决问题.
PB,把问题转化为垂线段最短即可解决问题.
(3)在旋转过程中,符号条件的△GD0H有8种情形,分别画出图形一一求解即可.
(1)如图1中,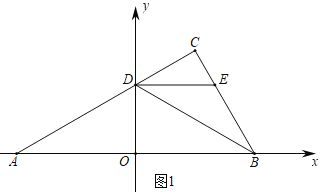
在Rt△AOD中,∵∠AOD=90°,∠OAD=30°,OD=2![]() ,
,
∴OA=![]() OD=6,∠ADO=60°,
OD=6,∠ADO=60°,
∴∠ODC=120°,
∵BD平分∠ODC,
∴∠ODB=![]() ∠ODC=60°,
∠ODC=60°,
∴∠DBO=∠DAO=30°,
∴DA=DB=4![]() ,OA=OB=6,
,OA=OB=6,
∴A(-6,0),D(0,2![]() ),B(6,0),
),B(6,0),
∴直线AC的解析式为y=![]() x+2
x+2![]() ,
,
∵AC⊥BC,
∴直线BC的解析式为y=-![]() x+6
x+6![]() ,
,
由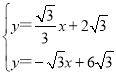 ,解得
,解得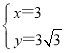 ,
,
∴C(3,3![]() ).
).
(2)如图2中,设BD交O′D′于G,交A′D′于F.作PH⊥OB于H.
∵∠FD′G=∠D′GF=60°,
∴△D′FG是等边三角形,
∵S△D′FG=![]() ,
,
∴D′G=![]() ,
,
∴DD′=![]() GD′=2,
GD′=2,
∴D′(2,2![]() ),
),
∵C(3,3![]() ),
),
∴CD′=![]() =2,
=2,
在Rt△PHB中,∵∠PHB=90°,∠PBH=30°,
∴PH=![]() PB,
PB,
∴CD'+D'P+![]() PB=2+D′P+PH≤2+D′O′=2+2
PB=2+D′P+PH≤2+D′O′=2+2![]() ,
,
∴CD'+D'P+![]() PB的最小值为2+2
PB的最小值为2+2![]() .
.
(3)如图3-1中,当D0H⊥GH时,连接ED0.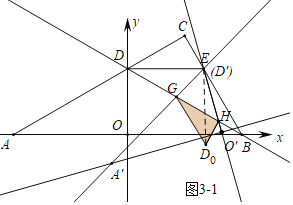
∵ED=ED0,EG=EG.DG=D0G,
∴△EDG≌△ED0G(SSS),
∴∠EDG=∠ED0G=30°,∠DEG=∠D0EG,
∵∠DEB=120°,∠A′EO′=60°,
∴∠DEG+∠BEO′=60°,
∵∠D0EG+∠D0EO′=60°,
∴∠D0EO′=∠BEO′,
∵ED0=EB,E=EH,
∴△EO′D0≌△EO′B(SAS),
∴∠ED0H=∠EBH=30°,HD0=HB,
∴∠CD0H=60°,
∵∠D0HG=90°,
∴∠D0GH=30°,设HD0=BH=x,则DG=GD0=2x,GH=![]() x,
x,
∵DB=4![]() ,
,
∴2x+![]() x+x=4
x+x=4![]() ,
,
∴x=2![]() -2.
-2.
如图3-2中,当∠D0GH=90°时,同法可证∠D0HG=30°,易证四边形DED0H是等腰梯形,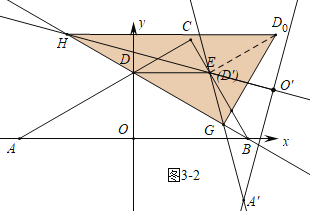
∵DE=ED0=DH=4,可得D0H=4+2×4×cos30°=4+4![]() .
.
如图3-3中,当D0H⊥GH时,同法可证:∠D0GH=30°,
在△EHD0中,由∠D0HE=45°,∠HD0E=30°,ED0=4,可得D0H=4×![]() ,
,
如图3-4中,当DG⊥GH时,同法可得∠D0HG=30°,
设DG=GD0=x,则HD0=BH=2x,GH=![]() x,
x,
∴3x+![]() x=4
x=4![]() ,
,
∴x=2![]() -2,
-2,
∴D0H=2x=4![]() -4.
-4.
如图3-5中,当D0H⊥GH时,同法可得D0H=2![]() -2.
-2.
如图3-6中,当DGG⊥GH时,同法可得D0H=4![]() +4.
+4.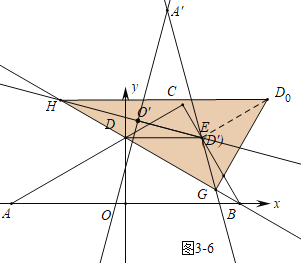
如图3-7中,如图当D0H⊥HG时,同法可得D0H=2![]() +2.
+2.
如图3-8中,当D0G⊥GH时,同法可得HD0=4![]() -4.
-4.
综上所述,满足条件的D0H的值为2![]() -2或2
-2或2![]() +2或4
+2或4![]() -4或4
-4或4![]() +4.
+4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
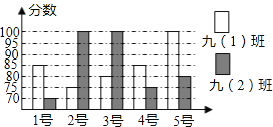
【题目】我区某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:
(1)九(1)班复赛成绩的中位数是 分,九(2)班复赛成绩的众数是 分;
(2)小明同学已经算出了九(1)班复赛的平均成绩![]() =85分;方差S2=
=85分;方差S2=![]() [(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
(3)根据(2)中计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
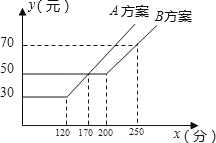
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
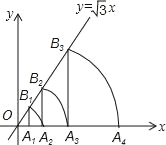
【题目】如图,已知直线y=![]() x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,求点B6的坐标.
x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,求点B6的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,
,![]() 的面积为48.
的面积为48.
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,连接
上,连接![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,如图3,连接![]() ,点
,点![]() 为
为![]() 轴正半轴上点
轴正半轴上点![]() 右侧一点,点
右侧一点,点![]() 为第一象限内一点,
为第一象限内一点,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,直线
上一点,直线![]() 经过点
经过点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,请你判断四边形
,请你判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com