练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

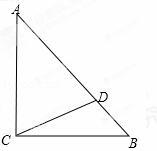
    如图，在△ABC中，∠ACB=90°，AC=BC=AD．

    （1）作∠A的平分线交CD于E；

    （2）过B作CD的垂线，垂足为F；

    （3）请写出图中两对全等三角形（不添加任何字母），并选择其中一对加以证明．


    解:（1）（2）作图如下

       (3)△ACE≌△ADE,△ACE≌△CFB

       证明:△ACE≌△ADE

       ∵AE是∠A的平分线,

       ∴∠CAE=∠DAE,

       又AC=AD,AE为公共边,

       ∴△ACE≌△ADE(SAS).


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列计算正确的是（　　）

    　  A．x4+x4=x16      B． （﹣2a）2=﹣4a2  C． x7÷x5=x2         D． m2•m3=m6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


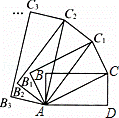
    如图，在矩形ABCD中，AD=2，CD=1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB1C1C，再连接AC1，以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1，…，按此规律继续下去，则矩形ABnCnCn﹣1的面积为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在⊙O中，直径AB⊥CD，垂足为E，∠BOD=48°，则∠BAC的大小是（　　）

    A．60°      B．48°      C．30°      D．24°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


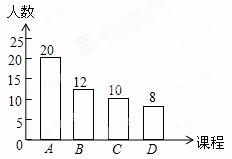
    某学校计划开设A，B，C，D四门校本课程供学生选修，规定每个学生必须并且只能选修其中一门，为了了解学生的选修意向，现随机抽取了部分学生进行调查，并将调查结果绘制成如图所示的条形统计图，已知该校学生人数为2000人，由此估计选修A课程的学生有          人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


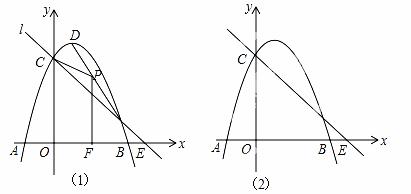
    如图1，抛物线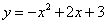与x轴交于A，B，与y轴交于C，抛物线的顶点为D，直线l过C交x轴于E（4，0）．

    （1）写出D的坐标和直线l的解析式；

    （2）P（x，y）是线段BD上的动点（不与B，D重合），PF⊥x轴于F，设四边形OFPC的面积为S，求S与x之间的函数关系式，并求S的最大值；

    （3）点Q在x轴的正半轴上运动，过Q作y轴的平行线，交直线l于M，交抛物线于N，连接CN，将△CMN沿CN翻转，M的对应点为M′．在图2中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个几何体的三视图如图所示，则该几何体的形状可能是

    查看答案和解析>>

    科目：初中数学 来源： 题型：


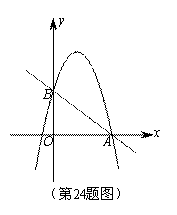
    如图，已知二次函数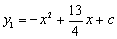的图象与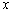轴的一个交点为A（4，0），与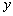轴的交点为B，过A、B的直线为。

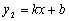        （1）求二次函数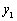的解析式及点B的坐标；

        （2）由图象写出满足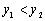的自变量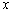的取值范围；

        （3）在两坐标轴上是否存在点P，使得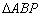是以AB为底边的等腰三角形？若存在，

    求出P点的坐标；若不存在，请说明理由。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    点（﹣1，y1）、（2，y2〕是直线y=2x+1上的两点，则y1　 　y2（填“＞”或“=”或“＜”）

     

    查看答案和解析>>

    同步练习册答案