
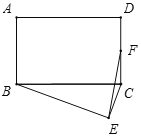
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A. 8B. 9C. 10D. 2![]()
【答案】B
【解析】
取BC中点O,连接OE,OF,根据矩形的性质可求OC,CF的长,根据勾股定理可求OF的长,根据直角三角形的性质可求OE的长,根据三角形三边关系可求得当点O,点E,点F共线时,EF有最大值,即EF=OE+OF.
解:如图,取BC中点O,连接OE,OF,

∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠C=90°,
∵点F是CD中点,点O是BC的中点,
∴CF=3,CO=4,
∴OF=![]() =5,
=5,
∵点O是Rt△BCE的斜边BC的中点,
∴OE=OC=4,
∵根据三角形三边关系可得:OE+OF≥EF,
∴当点O,点E,点F共线时,EF最大值为OE+OF=4+5=9.
故选:B.


科目:初中数学 来源: 题型:
【题目】在学习了一次函数图像后,张明、李丽和王林三位同学在赵老师的指导下,对一次函数![]() 进行了探究学习,请根据他们的对话解答问题.
进行了探究学习,请根据他们的对话解答问题.
(1)张明:当![]() 时,我能求出直线与
时,我能求出直线与![]() 轴的交点坐标为 ;
轴的交点坐标为 ;
李丽:当![]() 时,我能求出直线与坐标轴围成的三角形的面积为 ;
时,我能求出直线与坐标轴围成的三角形的面积为 ;
(2)王林:根据你们的探究,我发现无论![]() 取何值,直线总是经过一个固定的点,请求出这个定点的坐标.
取何值,直线总是经过一个固定的点,请求出这个定点的坐标.
(3)赵老师:我来考考你们,如果点![]() 的坐标为
的坐标为![]() ,该点到直线
,该点到直线![]() 的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.
的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a<0)经过A(2,4)、B(﹣1,1)两点,顶点坐标为(h,k),则下列正确结论的序号是( )
①b>1;②c>2;③h>![]() ;④k≤1.
;④k≤1.
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
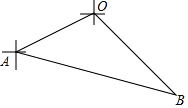
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

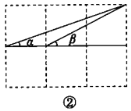
(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com