
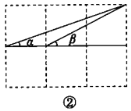
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).
科目:初中数学 来源: 题型:
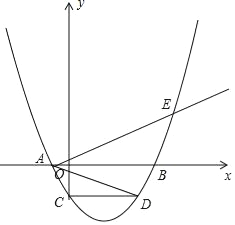
【题目】如图,二次函数y=a(x2﹣4mx﹣12m2)(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣6),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2)求证:![]() 为定值;
为定值;
(3)设该二次函数图象的顶点为F,连接FC并延长交x轴的负半轴于点G,判断以线段GF、AD、AE的长度为三边长的三角形的面积是否能为24(![]() +1)m2﹣48
+1)m2﹣48![]() m﹣72
m﹣72![]() +24,能则求出m;不能则说明理由.
+24,能则求出m;不能则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
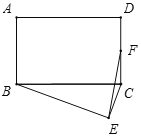
A. 8B. 9C. 10D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市在城市建设中,要折除旧烟囱![]() ,在烟囱正西方向的楼
,在烟囱正西方向的楼![]() 的顶端
的顶端![]() ,测得烟囱的顶端
,测得烟囱的顶端![]() 的仰角为
的仰角为![]() ,底端
,底端![]() 的俯角为
的俯角为![]() ,已量得
,已量得![]() .拆除时若让烟囱向正东倒下,试问:距离烟囱东方
.拆除时若让烟囱向正东倒下,试问:距离烟囱东方![]() 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形ABCD,其中AD//BC,坡长AB=10cm,坡角![]() ,汛期来临前对其进行了加固,改造后的背水面坡角
,汛期来临前对其进行了加固,改造后的背水面坡角![]() .(注:请在结果中保留根号)
.(注:请在结果中保留根号)
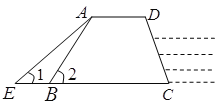
(1)试求出防洪大堤的横断面的高度;
(2)请求出改造后的坡长AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,
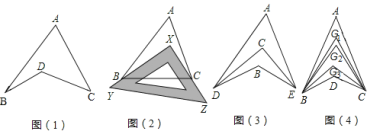
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX等于多少度;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
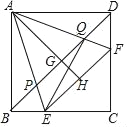
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
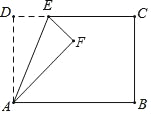
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )
①△EFP的外接圆的圆心为点G;
②四边形AEFB的面积不变;
③EF的中点G移动的路径长为4.
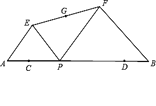
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com