
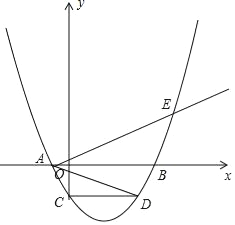
����Ŀ����ͼ�����κ���y=a��x2��4mx��12m2��������a��m�dz�������a��0��m��0����ͼ����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ��C��0����6������D�ڶ��κ�����ͼ���ϣ�CD��AB������AD������A������AE�����κ�����ͼ���ڵ�E��ABƽ�֡�DAE��
��1���ú�m�Ĵ���ʽ��ʾa��
��2����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
��3����ö��κ���ͼ��Ķ���ΪF������FC���ӳ���x��ĸ������ڵ�G���ж����߶�GF��AD��AE�ij���Ϊ���߳��������ε�����Ƿ���Ϊ24��![]() +1��m2��48
+1��m2��48![]() m��72
m��72![]() +24���������m��������˵�����ɣ�
+24���������m��������˵�����ɣ�
���𰸡���1��a=![]() ����2������������3��m=3��
����2������������3��m=3��
��������
��1���ѵ�C�������y=a��x2��4mx��12m2���У����ɽ�����⣮
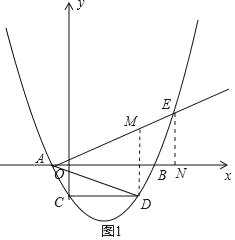
��2����ͼ1������D��E�ֱ���x��Ĵ��ߣ�����ΪM��N���������A��B�������꣬�ɡ�ADM�ס�AEN���Ƴ�![]() ��E����Ϊ
��E����Ϊ![]() �ɵ�
�ɵ�![]() �Ƴ�x=8m���ɵ�E��8m��10������AM=AO+OM=2m+4m=6m��AN=AO+ON=2m+8m=10m���ɴ˼��ɽ�����⣮
�Ƴ�x=8m���ɵ�E��8m��10������AM=AO+OM=2m+4m=6m��AN=AO+ON=2m+8m=10m���ɴ˼��ɽ�����⣮
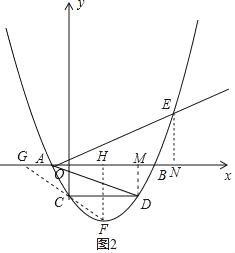
��3����ͼ2���Ƕ��κ���ͼ��ΪF����F������Ϊ��m��-4��������F��FH��x���ڵ�H������FC���ӳ�����x�Ḻ���ύ��һ�㣬�˵㼴Ϊ����ĵ�G��
��![]() �Ƴ�
�Ƴ�![]() ��
��![]() �õ�OG=6m��
�õ�OG=6m��![]() �ɵ�
�ɵ�
AD��GF��AE=3��4��5���ɴ˼��ɽ�����⣮
��1����C��0����6����������y=a��x2��4mx��12m2����
��6=a��0��0��12m2����
���a=![]() ��
��
��2��֤������ͼ1������D��E�ֱ���x��Ĵ��ߣ�����ΪM��N��
��a��x2��4mx��12m2��=0��
���x1=��2m��x2=6m��
���A����2m��0����B��6m��0����
��CD��AB��
���D��������4m����6����
��ABƽ�֡�DAE��
���DAM=��EAN��
���DMA=��ENA=90�㣬
���ADM�ס�AEN��
��![]()
���E����Ϊ![]()
![]()
��x=8m��
��E��8m��10����
��AM=AO+OM=2m+4m=6m��AN=AO+ON=2m+8m=10m��
��![]() ��Ϊ��ֵ��
��Ϊ��ֵ��
��3����ͼ2���Ƕ��κ���ͼ��Ķ���ΪF����F������Ϊ��2m����8��������F��FH��x���ڵ�H��
��![]()
��![]() ��
��![]()
��OG=6m��
��![]()
��![]()
��![]()
��AD��GF��AE=3��4��5��
�����߶�GF��AD��AE�ij���Ϊ���߳�����������ֱ�������Σ�
�����߶�GF��AD��AE�ij���Ϊ���߳��������ε����Ϊ![]()
��![]()
��m=3��m=��1��
��m��0��
��m=3��


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����ǧ�ܣ���ͼ�Ǵ����濴������ǧ������Ȼ�´�ʱ��̤�������0.5m��̤���Ⱥ��Բ��ƣ��� ��ͼ�ǴӲ��濴������ǧ̤�嵴������Bλ��ʱ����B����洹ֱ�߶�BCΪ1m������ǧ֧��AD��ˮƽ����BEΪ1.5m��������֧����ֱ����.����ǧ֧��AD�ĸ�.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() ��
��
��1�����˷��̵�һ����Ϊ1����![]() ��ֵ��
��ֵ��
��2����֤������![]() ȡ��ʵ�����˷��̶�����������ȵ�ʵ������
ȡ��ʵ�����˷��̶�����������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ�� ![]() ��
��![]() ��
��![]() ������
������
���������ʽ��ӳ�Ĺ��ɣ�����������⣺
��1�������������ʽ��������������������ͬһ��ʵ���� ![]() �� ��-5=�� ��
�� ��-5=�� ��![]() ��
��
��2��С����������ʽ����������ĸ��ʾΪ��![]() ��
��![]() ��
��![]() Ϊ����ʵ����.
Ϊ����ʵ����.
��С����ͬѧ���ۺ��֣�![]() ��
��![]() ��ȡֵ��Χ����������ʵ��.����ֱ��д��
��ȡֵ��Χ����������ʵ��.����ֱ��д��![]() ��
��![]() ����ȡ��Щʵ��.
����ȡ��Щʵ��.
���Ƿ����![]() ��
��![]() ����ʵ����������������������ڣ������
����ʵ����������������������ڣ������![]() ��
��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
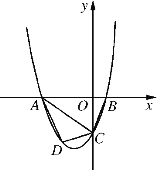
����Ŀ����֪����ͼ2211������y��ax2��2ax��c(a>0)��y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣮��B������Ϊ(1,0)��OC��3OB.
��1���������ߵĽ���ʽ��
��2������D���߶�AC�·��������ϵĶ��㣬���ı���ABCD��������ֵ��
��3�������������Ƿ����һ��P,ʹ![]() �������ڣ������������ꣻ����������˵������.
�������ڣ������������ꣻ����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ1��������ABCD����A��0��1����B��1��1����һ������y=ax2+bx+c����M����1��0���Ҷ�����������ABCD�ڲ��������������εı��ϣ�����a��ȡֵ��Χ�ǣ�������
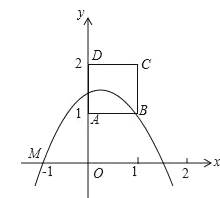
A. ��2��a�ܩ�1 B. ��2��a�ܩ�![]() C. ��1��a�ܩ�
C. ��1��a�ܩ�![]() D. ��1��a�ܩ�
D. ��1��a�ܩ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ��һ�κ���ͼ���,������������������λͬѧ������ʦ��ָ����,��һ�κ���![]() ������̽��ѧϰ,��������ǵĶԻ��������.
������̽��ѧϰ,��������ǵĶԻ��������.
(1)����:��![]() ʱ,�������ֱ����
ʱ,�������ֱ����![]() ��Ľ�������Ϊ ;
��Ľ�������Ϊ ;
����:��![]() ʱ,�������ֱ����������Χ�ɵ������ε����Ϊ ;
ʱ,�������ֱ����������Χ�ɵ������ε����Ϊ ;
(2)����:�������ǵ�̽��,�ҷ�������![]() ȡ��ֵ,ֱ�����Ǿ���һ���̶��ĵ�,�����������������.
ȡ��ֵ,ֱ�����Ǿ���һ���̶��ĵ�,�����������������.
(3)����ʦ:������������,�����![]() ������Ϊ
������Ϊ![]() ,�õ㵽ֱ��
,�õ㵽ֱ��![]() �ľ���������ֵ��?������,����������ֵ;��������,��˵������.
�ľ���������ֵ��?������,����������ֵ;��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߣ�y=ax2+bx+c��a��0������A��2��4����B����1��1�����㣬��������Ϊ��h��k������������ȷ���۵�����ǣ�������
��b��1����c��2����h��![]() ����k��1��
����k��1��
A. �٢ڢۢ� B. �٢ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������6����С��ͬ��С��������ɵķ����У���ÿ��С�����εı߳���Ϊ1.
��1����ͼ�٣�![]() ��
��![]() ��
��![]() ��������㣨��С�����εĶ��㣩���ж�
��������㣨��С�����εĶ��㣩���ж�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�

��2����ͼ�ڣ��������������ĶԽ��ߣ���![]() �Ķ�����Ҫ����ʾ��ͼ����д��֤�����̣�.
�Ķ�����Ҫ����ʾ��ͼ����д��֤�����̣�.
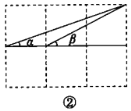
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com