
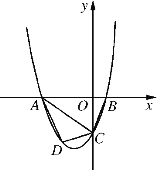
【题目】已知,如图2211抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)抛物线线上是否存在一点P,使![]() ,若存在,请求出点的坐标;若不存在请说明理由.
,若存在,请求出点的坐标;若不存在请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在点P,
;(3)存在点P,![]() 或
或![]() .
.
【解析】
①已知B坐标,可求得OB,OC,再将B,C坐标带入抛物线,即可求出解析式;
②根据A,C坐标可求直线解析式,由于AB,OC为定值吗,则△ABC面积不变,若四边形ABCD面积最大,则三角形的面积最大,可过D作x轴的垂线,可知△ADC的面积为DMYU OA积的一半,可设N坐标,分别带入AC和抛物线解析式,可求DM长度,进而求四边形ABCD的面积与N点横坐标间的函数关系,根据函数性质即可求出四边形ABCD的最大面积;
③本题分情况讨论1、过C作x轴的平行线,与抛物线的交点符合P点的要求,此时P,C的纵坐标相同,带入抛物线的解析式即可;2、将AC平移,令C点落在x轴,A点落到抛物线上,根据平行四边形性质,得出P点纵坐标,带入抛物线解析式可求P点坐标.
(1)![]()
![]()
(2)令![]() ,即
,即![]()
![]()
![]() 点A为(-3,0)
点A为(-3,0)
易求AC的解析式为![]() ,过点
,过点![]() 于H交AC于E
于H交AC于E
设点D为![]() ,则点E为
,则点E为![]() ,
,![]()
设面积S,![]()
![]() 当
当![]() 时,
时,![]() .
.
(3)存在点P,![]() 或
或![]()


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
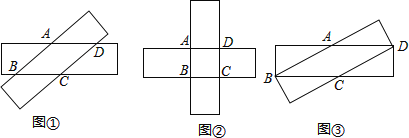
【题目】小宇将两张长为8宽为2的矩形条交叉如图①,发现重叠部分可能是一个菱形.
(1)请你帮助小宇证明四边形ABCD是菱形.
(2)小宇又发现:如图②时,菱形ABCD的周长最小,等于 ;
(3)如图③时菱形ABCD的周长最大,求此时菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
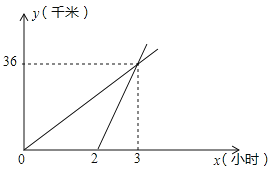
【题目】甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程![]() (千米)与小聪行驶的时间
(千米)与小聪行驶的时间![]() (小时)之间的函数关系如图所示,小明父亲出发多少小时,行进中的两车相距8千米.
(小时)之间的函数关系如图所示,小明父亲出发多少小时,行进中的两车相距8千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论正确的有( )个
,下列结论正确的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等腰三角形;⑤
是等腰三角形;⑤![]() .
.

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
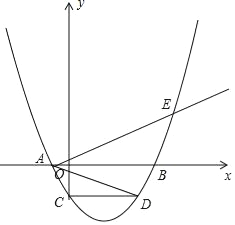
【题目】如图,二次函数y=a(x2﹣4mx﹣12m2)(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣6),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2)求证:![]() 为定值;
为定值;
(3)设该二次函数图象的顶点为F,连接FC并延长交x轴的负半轴于点G,判断以线段GF、AD、AE的长度为三边长的三角形的面积是否能为24(![]() +1)m2﹣48
+1)m2﹣48![]() m﹣72
m﹣72![]() +24,能则求出m;不能则说明理由.
+24,能则求出m;不能则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
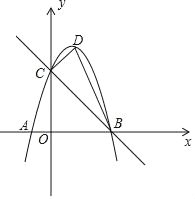
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形ABCD,其中AD//BC,坡长AB=10cm,坡角![]() ,汛期来临前对其进行了加固,改造后的背水面坡角
,汛期来临前对其进行了加固,改造后的背水面坡角![]() .(注:请在结果中保留根号)
.(注:请在结果中保留根号)
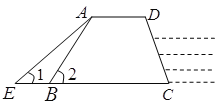
(1)试求出防洪大堤的横断面的高度;
(2)请求出改造后的坡长AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com