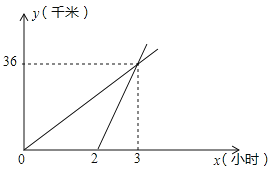
【题目】甲乙两地相距50千米.星期天上午8：00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后，小明的父亲骑摩托车沿同一路线也从甲地前往乙地，他们行驶的路程
（千米）与小聪行驶的时间
（小时）之间的函数关系如图所示，小明父亲出发多少小时，行进中的两车相距8千米.
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：
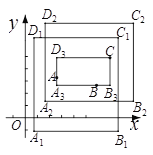
若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的外延矩形．点A，B，C的所有外延矩形中，面积最小的矩形称为点A，B，C的最佳外延矩形．例如，图中的矩形
，
，
都是点A，B，C的外延矩形，矩形是点A，B，C的最佳外延矩形．
（1）如图1，已知A（－2，0），B（4，3），C（0，
）．
①若
，则点A，B，C的最佳外延矩形的面积为 ；
②若点A，B，C的最佳外延矩形的面积为24，则的值为 ；
（2）如图2，已知点M（6，0），N（0，8）．P（
，
）是抛物线
上一点，求点M，N，P的最佳外延矩形面积的最小值，以及此时点P的横坐标的取值范围；
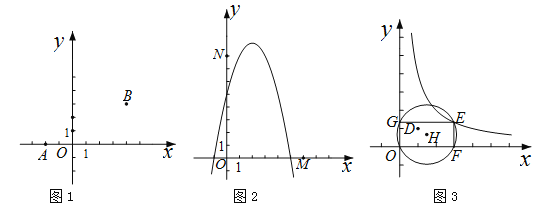
（3）如图3，已知点D（1，1）．E（
，
）是函数
的图象上一点，矩形OFEG是点O，D，E的一个面积最小的最佳外延矩形，⊙H是矩形OFEG的外接圆，请直接写出⊙H的半径r的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读：对于所有的一元二次方程ax2+bx+c＝0（a≠0）中，对于两根x1，x2，存在如下关系：x1+x2＝
，x1x2＝
．试着利用这个关系解决问题．设方程2x2﹣5x﹣3＝0的两根为x1，x2，不解方程，求下列式子的值：2x12+4x22+5x1．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c的图象经过点（0，1），对称轴为直线x=﹣1，下列结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④4a﹣2b+c＞0；⑤c﹣a＞1．其中，正确结论的个数为（ ）
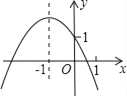
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列等式： 
；
；
；……
根据上面等式反映的规律，解答下列问题：
（1）请根据上述等式的特征，在括号内填上同一个实数： 
（ ）-5=（ ）
；
（2）小明将上述等式的特征用字母表示为：
（
、
为任意实数）.
①小明和同学讨论后发现：、的取值范围不能是任意实数.请你直接写出、不能取哪些实数.
②是否存在、两个实数都是整数的情况？若存在，请求出、的值；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
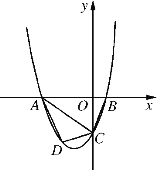
【题目】已知，如图2211抛物线y＝ax2＋2ax＋c(a>0)与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为(1,0)，OC＝3OB.
（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）抛物线线上是否存在一点P,使
，若存在，请求出点的坐标；若不存在请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习了一次函数图像后,张明、李丽和王林三位同学在赵老师的指导下,对一次函数
进行了探究学习,请根据他们的对话解答问题.
(1)张明:当
时,我能求出直线与
轴的交点坐标为 ;
李丽:当
时,我能求出直线与坐标轴围成的三角形的面积为 ;
(2)王林:根据你们的探究,我发现无论
取何值,直线总是经过一个固定的点,请求出这个定点的坐标.
(3)赵老师:我来考考你们,如果点
的坐标为
,该点到直线的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
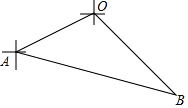
【题目】如图，甲、乙两渔船同时从港口O出发外出捕鱼，乙沿南偏东30°方向以每小时10海里的速度航行，甲沿南偏西75°方向以每小时10
海里的速度航行，当航行1小时后，甲在A处发现自己的渔具掉在乙船上，于是迅速改变航向和速度，仍以匀速沿南偏东60°方向追赶乙船，正好在B处追上．则甲船追赶乙船的速度为________海里/小时？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
