
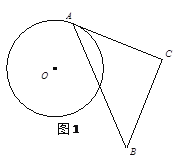
����Ŀ����ͼ����֪AB=12����C��D��AB�ϣ���AC=DB=2����P�ӵ�C���߶�CD���D�˶����˶�����Dֹͣ������AP��BPΪб����AB��ͬ�����Rt��APE�͵���Rt��PBF������EF��ȡEF���е�G������˵������ȷ���У� ��
�١�EFP�����Բ��Բ��Ϊ��G��
���ı���AEFB��������䣻
��EF���е�G�ƶ���·����Ϊ4��
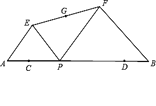
A. 0�� B. 1�� C. 2�� D. 3��
���𰸡�C
��������
������ͼ���ֱ��ӳ�AE��BF���ڵ�H��
������Rt��APE�͵���Rt��PBF�����A=��FPB=45������B=��EPA=45������AH��PF��BH��PE����EPF=180�㩁��EPA����FPB=90�������ı���EPFHΪƽ���ı��Σ���EF��HP����ƽ�֣���GΪEF���е㣬��GҲΪPH�е㣬����P���˶������У�Gʼ��ΪPH���е㣬��G�����й켣Ϊ��HCD����λ��MN����CD=12��2��2=8����MN=4����G���ƶ�·����Ϊ4������EF���е�G�ƶ���·����Ϊ4����ȷ��
��GΪEF���е㣬��EPF=90������١�EFP�����Բ��Բ��Ϊ��G����ȷ����٢���ȷ��
����PG����PG��PF�����EFP�����Բ��AB�ཻ����������
����P�ӵ�C���߶�CD���D�˶����˶�����Dֹͣ������֤��EPF=90���������ı��������������ֱ�������ε�����ͣ���cp=x�����ı������S=![]() ����AP�����������ı��ε����SҲ����֮�仯����������
����AP�����������ı��ε����SҲ����֮�仯����������
��ѡB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
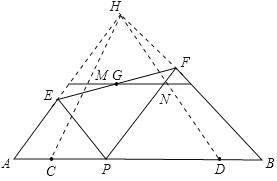
����Ŀ����ͼ������6����С��ͬ��С��������ɵķ����У���ÿ��С�����εı߳���Ϊ1.
��1����ͼ�٣�![]() ��
��![]() ��
��![]() ��������㣨��С�����εĶ��㣩���ж�
��������㣨��С�����εĶ��㣩���ж�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�

��2����ͼ�ڣ��������������ĶԽ��ߣ���![]() �Ķ�����Ҫ����ʾ��ͼ����д��֤�����̣�.
�Ķ�����Ҫ����ʾ��ͼ����д��֤�����̣�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD�ӳ����ϵ�һ�㣬BE=BA�����н��ۣ��١�ABD�ա�EBC���ڡ�BCE+��BCD=180�㣻��AD=AE=EC����AC=2CD��������ȷ���У� �� ����

A. 1 B. 2 C. 3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ5����ѧ�ɼ�ͳ����������ǵ�5���ܳɼ���ͬ��С���������ǵijɼ��������в�������ͳ��ͼ������ͬѧ������������⣮
���У�������ͼΪ���ߡ��ҵ�����ͼΪʵ�ߣ�
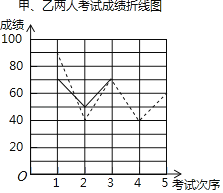
�ס������˵���ѧ�ɼ�ͳ�Ʊ�
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 | a | 70 |
��1��a���� ����![]() �� ����
�� ����
��2�������ͼ�б�ʾ�ҳɼ��仯��������ߣ�
��3��S2����260���ҳɼ��ķ������� �����ɿ����� ���ijɼ��Ƚ��ȶ�������������������������ƽ�����ͷ���ĽǶȷ������� ������ѡ�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=BC=8����PΪAB���е㣬EΪBC��һ���㣬��P����FP��PE��AC��F�㣬����P��E��F����ȷ����O��
��1����˵������CҲһ������O�ϣ�
��2����E���˶������У���PEF�Ķ����Ƿ�仯�������䣬�����PEF�Ķ��������仯��˵�����ɣ�
��3�����߶�EF��ȡֵ��Χ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC=90����D�DZ�AC�ϵ�һ�㣬����BD��ʹ��A=2��1��E��BC�ϵ�һ�㣬��BEΪֱ������O������D��

��1����֤��AC����O�����ߣ�
��2������A=60������O�İ뾶Ϊ2������Ӱ���ֵ������������������ź�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�麬��45�������ǰ�ABC�Ķ���A������O�ϣ���AC����O�����ڵ�A����ͼ1��������ABC�ӵ�A��ʼ�����ŵ�A˳ʱ����ת������ת��Ϊ����0��������135��������ת��AC��AB�ֱ�����O���ڵ�E��F������EF����ͼ2������֪AC=8����O�İ뾶Ϊ4��
��1������ת�����У������¼�����������EF�ij�����![]() �ij����ۡ�AFE�Ķ���������O��EF�ľ��룮���в��������___________________������ţ���
�ij����ۡ�AFE�Ķ���������O��EF�ľ��룮���в��������___________________������ţ���
��2��������________��ʱ��BC����O���У�ֱ��д���𰸣���
��3����BC����O����ʱ������AEF�������
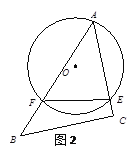
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������ϵ�е�λ����ͼ��ʾ������
������ϵ�е�λ����ͼ��ʾ������![]() �ᡢ
�ᡢ![]() ��Ľ���ֱ�Ϊ
��Ľ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ����Գ���
����Գ���![]() �ϵĶ��㣬����ͼ���ṩ����Ϣ���������½��ۣ���
�ϵĶ��㣬����ͼ���ṩ����Ϣ���������½��ۣ���![]() ����
����![]() ��
��![]() ��һ��������
��һ��������![]() �ܳ�����Сֵ��
�ܳ�����Сֵ��![]() ��������ȷ���ǣ� ��
��������ȷ���ǣ� ��
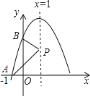
A. �����٢� B. �����ڢ� C. �����٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ����Ȥ������![]() .���������������2�����ʵ����ݱ䣬�����������˸��ŵ����棬���Dz��������������Ϊ����ǽ����������һ���ʵ����������࣬�磺
.���������������2�����ʵ����ݱ䣬�����������˸��ŵ����棬���Dz��������������Ϊ����ǽ����������һ���ʵ����������࣬�磺![]() ��
��![]() ��.
��.
��1�����룺![]() ______������֤��IJ��룮
______������֤��IJ��룮
��2������ֻ��һ��������![]() ����ʾ�����������ɵĵ�ʽ��
����ʾ�����������ɵĵ�ʽ��
��3������������д��1�����С���ǽ�����ʵ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com