
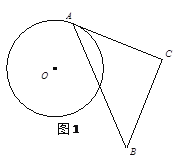
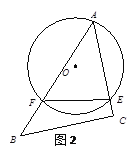
【题目】将一块含有45°的三角板ABC的顶点A放在⊙O上,且AC与⊙O相切于点A(如图1),将△ABC从点A开始,绕着点A顺时针旋转,设旋转角为α(0°<α<135°),旋转后,AC、AB分别与⊙O交于点E,F,连接EF(如图2).已知AC=8,⊙O的半径为4.
(1)在旋转过程中,有以下几个量:①弦EF的长;②![]() 的长;③∠AFE的度数;④点O到EF的距离.其中不变的量是___________________(填序号);
的长;③∠AFE的度数;④点O到EF的距离.其中不变的量是___________________(填序号);
(2)当α=________°时,BC与⊙O相切(直接写出答案);
(3)当BC与⊙O相切时,求△AEF的面积.
【答案】(1)①②④;(2)90°;(3)16.
【解析】
试题(1)连接EO,FO,可知三角形EOF为等腰直角三角形,作OD垂直EF于D,由垂径定理,勾股定理可得出结论;(2)因为AC=8,而⊙O的半径为4.所以当BC与⊙O相切时,△ACB绕点A旋转90°后AC恰为⊙O直径,即旋转角α为90度时BC与⊙O相切;(3)当BC与⊙O相切时,如图:点C与点E重合,AC为⊙O直径,利用三角形AEF是等腰直角三角形得出结果.
试题解析:(1)连接EO,FO,因为∠A=45,所以∠EOF=2∠A=90,因为EO=FO,所以三角形EOF为等腰直角三角形,作OD垂直EF于D,由垂径定理得:OD垂直平分EF,三角形ODE和三角形ODF是两个全等的等腰直角三角形,所以EF=![]() OF,OD=
OF,OD=![]() OF,而半径OF是一定的,所以弦EF的长不变,点O到EF的距离即OD不变,故①④正确,又因为半径不变,圆心角∠EOF=90不变,所以
OF,而半径OF是一定的,所以弦EF的长不变,点O到EF的距离即OD不变,故①④正确,又因为半径不变,圆心角∠EOF=90不变,所以![]() 的长不变,故②正确,而∠AFE的度数等于弧AE度数的一半,A点不变,E是旋转中AC与⊙O交点,可变,故弧AE度数可变,所以∠AFE的度数可变,故③错误,所以不变的序号应是①②④;(2)因为圆的切线垂直于过切点的半径,而∠ACB=90当BC与⊙O相切时,因为AC=8,而⊙O的半径为4.所以△ACB绕点A旋转90°后AC恰为⊙O直径,即旋转角α为90度时BC与⊙O相切;(3)如右图,
的长不变,故②正确,而∠AFE的度数等于弧AE度数的一半,A点不变,E是旋转中AC与⊙O交点,可变,故弧AE度数可变,所以∠AFE的度数可变,故③错误,所以不变的序号应是①②④;(2)因为圆的切线垂直于过切点的半径,而∠ACB=90当BC与⊙O相切时,因为AC=8,而⊙O的半径为4.所以△ACB绕点A旋转90°后AC恰为⊙O直径,即旋转角α为90度时BC与⊙O相切;(3)如右图,
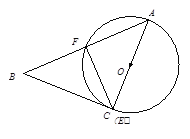
当BC与⊙O相切时,依题意可知,△ACB旋转90°后AC为⊙O直径,且点C与点E重合,∵AC为⊙O直径,∴∠AFE=90°.又∵∠BAC=45°,∴∠FCA=45°.∴∠BAC=∠FCA,∴AF=EF.∵AC=8,∴AF=EF=4![]() ,∴S△AEF=
,∴S△AEF=![]() ×(4
×(4![]() )2=16.故△AEF的面积是16..
)2=16.故△AEF的面积是16..


科目:初中数学 来源: 题型:
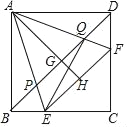
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
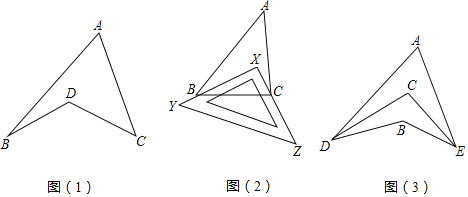
【题目】探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△ABC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX= °.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )
①△EFP的外接圆的圆心为点G;
②四边形AEFB的面积不变;
③EF的中点G移动的路径长为4.
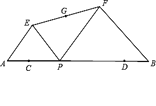
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“文化宜昌全民阅读”活动中,某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查,2012年全校有1000名学生,2013年全校学生人数比2012年增加10%,2014年全校学生人数比2013年增加100人.
(1)求2014年全校学生人数;
(2)2013年全校学生人均阅读量比2012年多1本,阅读总量比2012年增加1700本(注:阅读总量=人均阅读量×人数)
①求2012年全校学生人均阅读量;
②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2012年、2014年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2014年全校学生人均阅读量比2012年增加的百分数也是a,那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
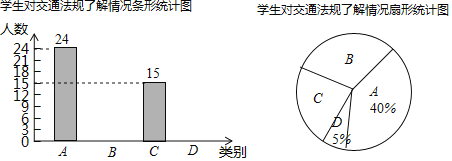
请结合图中所给信息解答下列问题:
(1)本次共调查 名学生;扇形统计图中C所对应扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有多少名?
(4)通过此次调查,数学课外实践小组的学生对交通法规有了更多的认识,学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求甲和乙两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
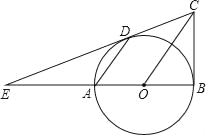
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,AD=5,求OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要把一批产品从A地运往B地,若通过铁路运输,则每千米需交运费15元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费25元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设A地到B地的路程为x km,通过铁路运输和通过公路运输需交总运费y1元和y2元,
(1)求y1和y2关于x的表达式.
(2)若A地到B地的路程为120km,哪种运输可以节省总运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;② 2a>b;③b=a+c;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.其中正确的命题有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com