
����Ŀ��̽���뷢�֣���ͼ��1����ʾ��ͼ�Σ������dz�����ѧϰ��ƷһԲ�棬���ǣ�����������ͼ�ν���������ͼ
��1���۲조����ͼ��1��������̽����BDC���A����B����C֮���������ϵ����˵�����ɣ�
��2������ֱ���������Ͻ��ۣ�����������⣺
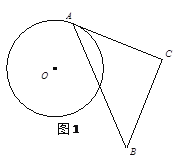
����ͼ��2������һ�����dz�XYZ�����ڡ�ABC��ʹ���dzߵ�����ֱ�DZ�XY��XZǡ�þ�����B��C������A��40�㣬���ABX+��ACX���� ���㣮
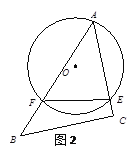
����ͼ��3����DCƽ�֡�ADB��ECƽ�֡�AEB������DAE��40�㣬��DBE��130�㣬���DCE�Ķ�����
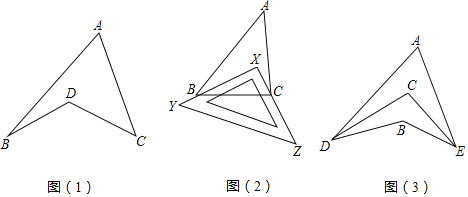
���𰸡���1����BDC����BAC+��B+��C�����ɼ���������2����50������DCE��85�㣮
��������
��1����������AD���ӳ�����F��Ȼ�������ǵ����ʣ������жϳ���BDC����BAC+��B+��C��
��2�����ɣ�1���ɵá�A+��ABX+��ACX����X��Ȼ����ݡ�A��40�㣬��X��90�㣬������⣻
��3�����ɡ�A��40�㣬��DBE��130�㣬�����ADE+��AEB��ֵ��Ȼ�������DCE����A+��ADC+��AEC�������DCE�Ķ�������.
��1����ͼ����BDC����BAC+��B+��C�������ǣ�
����A��D������AF��
�ߡ�FDC����DAC+��C����BDF����B+��BAD��
���FDC+��BDF����DAC+��BAD+��C+��B��
����BDC����BAC+��B+��C��
��2������ͼ��2�����ߡ�X��90�㣬
�ɣ�1��֪����A+��ABX+��ACX����X��90�㣬
�ߡ�A��40�㣬
���ABX+��ACX��50�㣬
�ʴ�Ϊ��50��
����ͼ��3�����ߡ�A��40�㣬��DBE��130�㣬
���ADE+��AEB��130�㩁40�㣽90�㣬
��DCƽ�֡�ADB��ECƽ�֡�AEB��
���ADC��![]() ��ADB����AEC��
��ADB����AEC��![]() ��AEB��
��AEB��
���ADC+��AEC��![]() ��45�㣬
��45�㣬
���DCE����A+��ADC+��AEC��40��+45�㣽85�㣮


 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס������洬ͬʱ�Ӹۿ�O����������㣬������ƫ��30��������ÿСʱ10������ٶȺ��У�������ƫ��75��������ÿСʱ10![]() ������ٶȺ��У�������1Сʱ����A�������Լ�����ߵ����Ҵ��ϣ�����Ѹ�ٸı亽����ٶȣ�������������ƫ��60���������Ҵ���������B���ϣ���״����Ҵ����ٶ�Ϊ________����/Сʱ��
������ٶȺ��У�������1Сʱ����A�������Լ�����ߵ����Ҵ��ϣ�����Ѹ�ٸı亽����ٶȣ�������������ƫ��60���������Ҵ���������B���ϣ���״����Ҵ����ٶ�Ϊ________����/Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
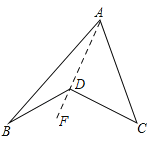
����Ŀ�� ��֪Rt��ABC�У�AC=BC����C=90�㣬DΪAB�ߵ��е㣬��EDF=90�㣬��EDF��D����ת���������߷ֱ�AC��CB�������ǵ��ӳ��ߣ���E��F������EDF��D����ת��DE��AC��Eʱ����ͼ1������֤![]() ������EDF��D����ת��DE��AC����ֱʱ����ͼ2��ͼ3����������£����������Ƿ����? �������������֤��������������
������EDF��D����ת��DE��AC����ֱʱ����ͼ2��ͼ3����������£����������Ƿ����? �������������֤��������������![]() ��
��![]() ��
��![]() ����������������ϵ����д����IJ��룬����֤����
����������������ϵ����д����IJ��룬����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD�ӳ����ϵ�һ�㣬BE=BA�����н��ۣ��١�ABD�ա�EBC���ڡ�BCE+��BCD=180�㣻��AD=AE=EC����AC=2CD��������ȷ���У� �� ����

A. 1 B. 2 C. 3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���E�ڱ�CD�ϣ����þ�����AE�۵���ʹ��D���ڱ�BC�ϵĵ�F��������F��FG��CD����AE�ڵ�G������DG��

��1����֤���ı���DEFGΪ���Σ�
��2����CD=8��CF=4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ5����ѧ�ɼ�ͳ����������ǵ�5���ܳɼ���ͬ��С���������ǵijɼ��������в�������ͳ��ͼ������ͬѧ������������⣮
���У�������ͼΪ���ߡ��ҵ�����ͼΪʵ�ߣ�
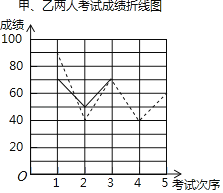
�ס������˵���ѧ�ɼ�ͳ�Ʊ�
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 | a | 70 |
��1��a���� ����![]() �� ����
�� ����
��2�������ͼ�б�ʾ�ҳɼ��仯��������ߣ�
��3��S2����260���ҳɼ��ķ������� �����ɿ����� ���ijɼ��Ƚ��ȶ�������������������������ƽ�����ͷ���ĽǶȷ������� ������ѡ�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
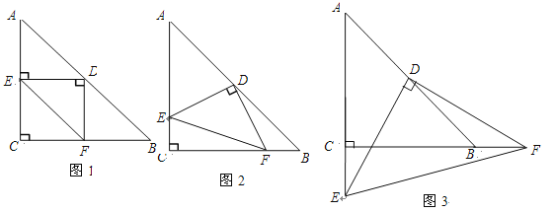
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=BC=8����PΪAB���е㣬EΪBC��һ���㣬��P����FP��PE��AC��F�㣬����P��E��F����ȷ����O��
��1����˵������CҲһ������O�ϣ�
��2����E���˶������У���PEF�Ķ����Ƿ�仯�������䣬�����PEF�Ķ��������仯��˵�����ɣ�
��3�����߶�EF��ȡֵ��Χ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�麬��45�������ǰ�ABC�Ķ���A������O�ϣ���AC����O�����ڵ�A����ͼ1��������ABC�ӵ�A��ʼ�����ŵ�A˳ʱ����ת������ת��Ϊ����0��������135��������ת��AC��AB�ֱ�����O���ڵ�E��F������EF����ͼ2������֪AC=8����O�İ뾶Ϊ4��
��1������ת�����У������¼�����������EF�ij�����![]() �ij����ۡ�AFE�Ķ���������O��EF�ľ��룮���в��������___________________������ţ���
�ij����ۡ�AFE�Ķ���������O��EF�ľ��룮���в��������___________________������ţ���
��2��������________��ʱ��BC����O���У�ֱ��д���𰸣���
��3����BC����O����ʱ������AEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�Ҵ���A���ر�ƫ��60��������10km��B�ۣ�Ȼ�����ر�ƫ��30��������10km��C�ۣ�
��1����A��C����֮��ľ��루���������0.1km���ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732����
��1.732����
��2��ȷ��C����A�۵�ʲô����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com