
【题目】如图,抛物线![]() 经过A(-3,0),C(5,0)两点,点B为抛物线顶点,抛物线的对称轴与x轴交于点D.
经过A(-3,0),C(5,0)两点,点B为抛物线顶点,抛物线的对称轴与x轴交于点D.
(1)求抛物线的解析式;
(2)动点P从点B出发,沿线段BD向终点D作匀速运动,速度为每秒1个单位长度,运动时间为t,过点P作PM⊥BD,交BC于点M,以PM为正方形的一边,向上作正方形PMNQ,边QN交BC于点R,延长NM交AC于点E.
①当t为何值时,点N落在抛物线上;
②在点P运动过程中,是否存在某一时刻,使得四边形ECRQ为平行四边形?若存在,求出此时刻的t值;若不存在,请说明理由.

【答案】(1)![]() ;(2)①t=4;②
;(2)①t=4;②![]()
【解析】试题分析:(1)把点A、C坐标代入抛物线解析式得到关于a、b的二元一次方程组,解方程组求出a、b的值,即可得解;
(2)根据抛物线解析式求出顶点B的坐标,然后根据相似三角形对应边成比例用t表示出PM,再求出NE的长度.①表示出点N的坐标,再根据点N在抛物线上,把点N的坐标代入抛物线,解方程即可得解;
②根据PM的长度表示出QD,再利用待定系数法求出直线BC的解析式,然后根据直线BC的解析式求出点R的横坐标,从而求出QR的长度,再表示出EC的长度,然后根据平行四边形对边平行且相等列式求解即可.
试题解析:解:(1)∵y=ax2+bx+![]() 经过A(﹣3,0),C(5,0)两点,∴
经过A(﹣3,0),C(5,0)两点,∴ ,解得:
,解得:  ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)∵![]() =﹣
=﹣![]() (x2﹣2x+1)+
(x2﹣2x+1)+![]() =﹣
=﹣![]() (x﹣1)2+8,∴点B的坐标为(1,8).设直线BC的解析式为y=kx+m,则
(x﹣1)2+8,∴点B的坐标为(1,8).设直线BC的解析式为y=kx+m,则![]() ,解得:
,解得: ![]() ,所以直线BC的解析式为y=﹣2x+10.∵抛物线的对称轴与x轴交于点D,∴BD=8,CD=5﹣1=4.∵PM⊥BD,∴PM∥CD,∴△BPM∽△BDC,∴
,所以直线BC的解析式为y=﹣2x+10.∵抛物线的对称轴与x轴交于点D,∴BD=8,CD=5﹣1=4.∵PM⊥BD,∴PM∥CD,∴△BPM∽△BDC,∴![]() ,即
,即![]() ,解得:PM=
,解得:PM=![]() t,∴OE=1+
t,∴OE=1+![]() t.∴ME=-2(1+
t.∴ME=-2(1+![]() t)+10=8-t..∵四边形PMNQ为正方形,∴NE=NM+ME=8﹣t+
t)+10=8-t..∵四边形PMNQ为正方形,∴NE=NM+ME=8﹣t+![]() t=8﹣
t=8﹣![]() t.
t.
①点N的坐标为(1+![]() t,8﹣
t,8﹣![]() t),若点N在抛物线上,则﹣
t),若点N在抛物线上,则﹣![]() (1+
(1+![]() t﹣1)2+8=8﹣
t﹣1)2+8=8﹣![]() t,整理得,t(t﹣4)=0,解得t1=0(舍去),t2=4,所以,当t=4秒时,点N落在抛物线上;
t,整理得,t(t﹣4)=0,解得t1=0(舍去),t2=4,所以,当t=4秒时,点N落在抛物线上;

②存在.理由如下:
∵PM=![]() t,四边形PMNQ为正方形,∴QD=NE=8﹣
t,四边形PMNQ为正方形,∴QD=NE=8﹣![]() t.∵直线BC的解析式为y=﹣2x+10,∴﹣2x+10=8﹣
t.∵直线BC的解析式为y=﹣2x+10,∴﹣2x+10=8﹣![]() t,解得:x=
t,解得:x=![]() t+1,∴QR=
t+1,∴QR=![]() t+1﹣1=
t+1﹣1=![]() t.又∵EC=CD﹣DE=4﹣
t.又∵EC=CD﹣DE=4﹣![]() t,根据平行四边形的对边平行且相等可得QR=EC,即
t,根据平行四边形的对边平行且相等可得QR=EC,即![]() t=4﹣
t=4﹣![]() t,解得:t=
t,解得:t=![]() ,此时点P在BD上,所以,当t=
,此时点P在BD上,所以,当t=![]() 时,四边形ECRQ为平行四边形.
时,四边形ECRQ为平行四边形.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,六个完全相同的小矩形排成一个大矩形,AB是其中一个小矩形的对角线,请在大矩形中完成下列画图,要求:①仅用无刻度直尺②保留必要的作图痕迹.
(1)在如图中画出与线段AB平行的线段CD
(2)在如图中画出过点A与线段AB垂直的线段AE
(3)在如图中画出线段AB的垂直平分线MN


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一根绳子平放在桌上,用剪刀任意剪n刀(如图①),绳子变成n+1段;若将绳子对折1次后从中间剪一刀(如图②),绳子的刀口 个,绳子变成 段;若将绳子对折2次后从中间剪一刀,绳子的刀口有 个,绳子变成 段;若将绳子对折n次后从中间剪一刀,绳子的刀口 个,绳子变成 段.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在数轴上表示的数分别为-4和+16,A,B两点间的距离可记为AB
![]()
(1) 点C在数轴上A,B两点之间,且AC=BC,则C点对应的数是_________
(2) 点C在数轴上A,B两点之间,且BC=4AC,则C点对应的数是_________
(3) 点C在数轴上,且AC+BC=30,求点C对应的数?
(4) 若点A在数轴上表示的数是a,B表示的数是b,则AB=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论是( )
.其中正确结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°.
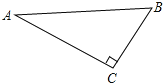
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com