
【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)
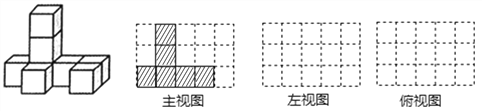
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<3),过点P作PD⊥BC于点D. ① 求线段PD的长的最大值;② 当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件概率为1的是( )
A.射击运动员射击一次,命中靶心
B.任意画一个三角形,其外角和是360°
C.篮球队员投篮一次未命中
D.丢一个骰子,向上一面的点数为7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com