Question

【题目】如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．

（1）求证：OE=OF；
（2）若BC=2 ，求AB的长．

Answer 1

【答案】
（1）

证明：在矩形ABCD中，AB∥CD，

∴∠BAC=∠FCO，

在△AOE和△COF中，

，

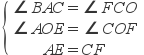∴△AOE≌△COF（AAS），

∴OE=OF；

（2）

解：如图，连接OB，

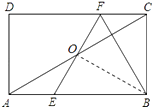
∵BE=BF，OE=OF，

∴BO⊥EF，

∴在Rt△BEO中，∠BEF+∠ABO=90°，

由直角三角形斜边上的中线等于斜边上的一半可知：OA=OB=OC，

∴∠BAC=∠ABO，

又∵∠BEF=2∠BAC，

即2∠BAC+∠BAC=90°，

解得∠BAC=30°，

∵BC=2 ，

∴AC=2BC=4 ，

∴AB= = =6．

【解析】（1）根据矩形的对边平行可得AB∥CD，再根据两直线平行，内错角相等求出∠BAC=∠FCO，然后利用“角角边”证明△AOE和△COF全等，再根据全等三角形的即可得证；（2）连接OB，根据等腰三角形三线合一的性质可得BO⊥EF，再根据矩形的性质可得OA=OB，根据等边对等角的性质可得∠BAC=∠ABO，再根据三角形的内角和定理列式求出∠ABO=30°，即∠BAC=30°，根据直角三角形30°角所对的直角边等于斜边的一半求出AC，再利用勾股定理列式计算即可求出AB．