
【题目】如图Rt△ABC中∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠DAC=22.5°,其中正确的是( )

A. ①②④B. ③④⑤C. ①③④D. ①②⑤
【答案】A
【解析】
①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;
②根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF;由此即可确定说法是否正确;
④据①BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.
⑤可以利用①②④正确,利用答案中没有更多正确答案,得出⑤错误.
①根据旋转的性质知∠CAD=∠BAF,AD=AF,
∵![]()
∴![]()
∴![]()
∴△AEF≌△AED;
故①正确;
②∵根据旋转的性质,∴△ADC≌△AFB,
∴△ABC的面积等于四边形AFBD的面积;
故此选项正确;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF,
∴BE+DC=BE+BF>DE=EF,
故③错误;
④∵AB=AC,△ADC旋转![]() 至△AFB,
至△AFB,
∴![]()
根据旋转的性质可得△ADC≌△AFB,![]()
∴![]()
∴![]()
∵△ADC绕点A顺时针旋转![]() 后,得到△AFB,
后,得到△AFB,
∴△AFB≌△ADC,
∴BF=CD,
又∵EF=DE,
∴![]() 故④正确.
故④正确.
⑤∵可以利用①②④正确,利用答案中没有更多正确答案,得出⑤错误.
故正确的有:①②④.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
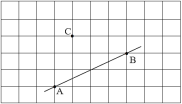
【题目】(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线__________的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段__________最短,理由:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
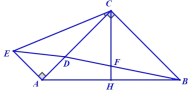
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CH为△ABC斜边上的中线,点F为CH上一点,连接BF并延长交AC于点D,过点A作AE⊥AC,连接CE和DE,若∠ACE=2∠ABF,CE=13,CD=8,则△CDE的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,共有“一白三黑”四个围棋子,其除颜色外无其他区别.
(1)随机地从盒子中取出1子,则提出的是白子的概率是多少?
(2)随机地从盒子中取出1子,不放回再取出第二子,请用画树状或列表的方式表示出所有可能的结果,并求出恰好取出“一黑一白”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,![]() ,
,![]() ,
,![]() .求
.求 ![]() 度数.
度数.
小明的思路是:如图2,过 ![]() 作
作 ![]() ,通过平行线性质,可得
,通过平行线性质,可得 ![]() .
.

问题迁移:
(1)如图3,![]() ,点
,点 ![]() 在射线
在射线 ![]() 上运动,当点
上运动,当点 ![]() 在
在 ![]() 、
、 ![]() 两点之间运动时,
两点之间运动时,![]() ,
,![]() .
.![]() 、
、 ![]() 、
、 ![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点 ![]() 在
在 ![]() 、
、 ![]() 两点外侧运动时(点
两点外侧运动时(点 ![]() 与点
与点 ![]() 、
、 ![]() 、
、 ![]() 三点不重合),请你直接写出
三点不重合),请你直接写出 ![]() 、
、 ![]() 、
、 ![]() 间的数量关系.
间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y= ![]() x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为( )
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为( )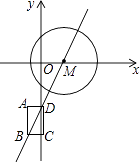
A.( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )
)
B.( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )
)
C.( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,﹣
,﹣ ![]() )
)
D.( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com