
【题目】已知:如图所示,在平面直角坐标系中,函数![]() (
(![]() ,
,![]() 是常数)的图象经过点
是常数)的图象经过点![]() 、点
、点![]() ,其中
,其中![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)求证:四边形![]() 为平行四边形;
为平行四边形;
(3)若![]() ,求直线
,求直线![]() 的函数解析式.
的函数解析式.

【答案】(1)点![]() ;(2)证明见解析;(3)直线
;(2)证明见解析;(3)直线![]() 的函数解析式为
的函数解析式为![]() 或
或![]() .
.
【解析】
(1)先用待定系数法求出双曲线解析式,再用点B在双曲线上得出ab=4,再用面积建立方程![]() a(4﹣b)=4,解方程组即可;
a(4﹣b)=4,解方程组即可;
(2)先求出直线AB解析式:y=﹣bx+b+4,再确定出DE,AC即可得到DE=AC,从而得出结论;
(3)由(2)知,AB∥CD,结合AD=BC,即可得出四边形ABCD是平行四边形或等腰梯形.分两种情况计算即可.
(1)将A(1,4)代入函数![]() 中,得:m=4,所以y
中,得:m=4,所以y![]() ;
;
∵S△ABD![]() BDAM
BDAM![]() a(4﹣b)=4.
a(4﹣b)=4.
∵B(a,b)在函数y![]() 的图象上,∴ab=4,∴a=3,b
的图象上,∴ab=4,∴a=3,b![]() ,即:点B(3,
,即:点B(3,![]() );
);
(2)∵函数y![]() (x>0,m是常数)的图象经过点A(1,4),∴m=4.
(x>0,m是常数)的图象经过点A(1,4),∴m=4.
∵B(a,b)在双曲线上,∴ab=4.
∵直线AB过点A(1,4),B(a,b),且ab=4,设直线AB解析式为y=ex+f,∴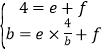 ,解得:e=-b,f=b+4,∴直线AB解析式为y=﹣bx+b+4,∴E(0,b+4).
,解得:e=-b,f=b+4,∴直线AB解析式为y=﹣bx+b+4,∴E(0,b+4).
∵BD⊥y轴,AC⊥x轴,∴D(0,b),∴DE=b+4﹣b=4.
∵A(1,4),∴AC=4,∴DE=AC.
∵DE∥AC,∴四边形ACDE为平行四边形;
(3)设直线AB的函数解析式为y=kx+b.
∵CD∥AB,AD=BC,∴四边形ABCD为平行四边形或等腰梯形.
情况1:四边形ABCD为平行四边形,则DM=MB,∴a﹣1=1,a=2,∴B(2,2).
∵A(1,4)、B(2,2)在直线AB上,∴直线AB解析式为:y=﹣2x+6;
情况2:四边形ABCD为等腰梯形,则AC=BD,∴a=4,∴B(4,1).
∵A(1,4)、B(4,1)在直线AB上,直线AB解析式为:y=﹣x+5.
综上所述:直线AB的函数解析式为y=﹣2x+6或y=﹣x+5.


科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:
(1)已知,△ABC中,∠C+∠A=4∠B,∠C﹣∠A=40°,则∠A= 度;∠B= 度;∠C= 度;
(2)一个多边形的内角和与外角和之和为2160°,则这个多边形是 边形;
(3)在如图的平面直角坐标系中,点A(﹣2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小.则点P的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
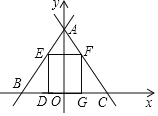
【题目】如图,直线y=kx+b与直线y=2x+6关于y轴对称且交于点A,直线y=2x+6交x轴于点B,直线y=kx+b交x轴于点C,正方形DEFG一边DG在线段BC上,点E在线段AB上,点F在线段AC上,则点G的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
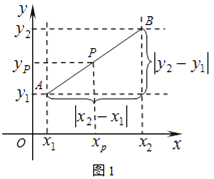
【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp﹣x1=x2﹣xp,得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为(![]() ,
,![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为________,MN=________.
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
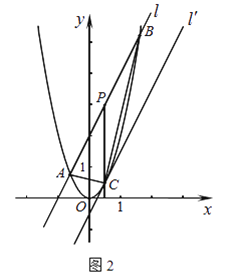
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
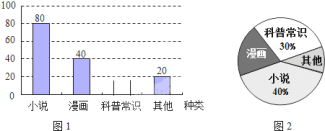
【题目】某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调查(每人只选一种书籍).图![]() 和图
和图![]() 是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次活动一共调查了________名学生;
(2)在图![]() 中,“漫画”所在扇形圆心角为________度;
中,“漫画”所在扇形圆心角为________度;
(3)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的![]() 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE。

(1)试说明△BDE≌△CDF
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
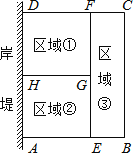
【题目】为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com