
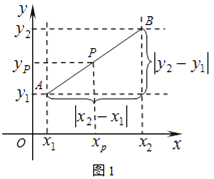
ЁОЬтФПЁПдФЖСВФСЯЃКШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊAЃЈx1 ЃЌ y1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌABжаЕуPЕФзјБъЮЊЃЈxpЃЌypЃЉЃЎгЩxpЉx1=x2ЉxpЃЌЕУxp= ![]() ЃЌЭЌРэyp=
ЃЌЭЌРэyp= ![]() ЃЌЫљвдABЕФжаЕузјБъЮЊЃЈ
ЃЌЫљвдABЕФжаЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎгЩЙДЙЩЖЈРэЕУAB2=|x2Љx1|2+|y2Љy1|2ЃЌЫљвдAЁЂBСНЕуМфЕФОрРыЙЋЪНЮЊAB=
ЃЉЃЎгЩЙДЙЩЖЈРэЕУAB2=|x2Љx1|2+|y2Љy1|2ЃЌЫљвдAЁЂBСНЕуМфЕФОрРыЙЋЪНЮЊAB=![]() ЃЎетСНЙЋЪНЖдAЁЂBдкЦНУцжБНЧзјБъЯЕжаЦфЫќЮЛжУвВГЩСЂЃЎНтД№ЯТСаЮЪЬтЃК
ЃЎетСНЙЋЪНЖдAЁЂBдкЦНУцжБНЧзјБъЯЕжаЦфЫќЮЛжУвВГЩСЂЃЎНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊMЃЈ1ЃЌЉ2ЃЉЃЌNЃЈЉ1ЃЌ2ЃЉЃЌжБНгРћгУЙЋЪНЬюПеЃКMNжаЕузјБъЮЊ________ЃЌMN=________ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпlЃКy=2x+2гыХзЮяЯпy=2x2НЛгкAЁЂBСНЕуЃЌPЮЊABЕФжаЕуЃЌЙ§PзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуCЃЎ
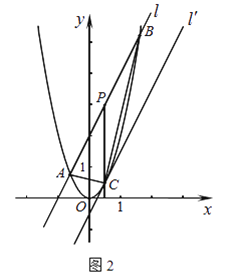
ЃЈaЃЉЧѓAЁЂBСНЕуЕФзјБъМАCЕуЕФзјБъЃЛ
ЃЈbЃЉСЌНсABЁЂACЃЌЧѓжЄЁїABCЮЊжБНЧШ§НЧаЮЃЛ
ЃЈcЃЉНЋжБЯпlЦНвЦЕНCЕуЪБЕУЕНжБЯпlЁфЃЌЧѓСНжБЯпlгыlЁфЕФОрРы.
ЁОД№АИЁПЃЈ1ЃЉЃЈ0ЃЌ0ЃЉЃЛ2![]() ЃЛЃЈ2ЃЉЃЈaЃЉAЃЈ
ЃЛЃЈ2ЃЉЃЈaЃЉAЃЈ ![]() ЃЌ3Љ
ЃЌ3Љ![]() ЃЉЃЛBЃЈ
ЃЉЃЛBЃЈ ![]() ЃЌ3+
ЃЌ3+![]() ЃЉЃЛ CЃЈ
ЃЉЃЛ CЃЈ ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈbЃЉжЄУїМћНтЮіЃЛЃЈcЃЉ
ЃЉЃЛЃЈbЃЉжЄУїМћНтЮіЃЛЃЈcЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжаЕузјБъЙЋЪНЃЌСНЕуМфЕФОрРыЙЋЪНЃЌПЩЕУД№АИЃЛ
ЃЈaЃЉИљОнНтЗНГЬзщЃЌПЩЕУAЃЌBЕузјБъЃЌИљОнжаЕузјБъЙЋЪНЃЌПЩЕУPЕузјБъЃЌИљОнЦНаагкyжсЕФжБЯпКсзјБъЯрЕШЃЌПЩЕУCЕуКсзјБъЃЌИљОнздБфСПгыКЏЪ§жЕЕФЖдгІЙиЯЕЃЌПЩЕУCЕузјБъЃЛ
ЃЈbЃЉИљОнЙДЙЩЖЈРэМАЙДЙЩЖЈРэЕФФцЖЈРэЃЌПЩЕУД№АИЃЛ
ЃЈcЃЉИљОнШ§НЧаЮЕФУцЛ§ВЛЭЌБэЪОЃЌПЩЕУЙигкCDЕФЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУД№АИЃЎ
ЃЈ1ЃЉЃЈ0ЃЌ0ЃЉЃЛ2![]()
ЃЈ2ЃЉНтЃКЃЈaЃЉСЊСЂжБЯпЁЂХзЮяЯпЃЌЕУ ![]() ЃЌ
ЃЌ
НтЕУ 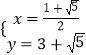 ЃЌ
ЃЌ 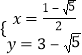 ЃЌ
ЃЌ
МДBЃЈ ![]() ЃЌ3+
ЃЌ3+![]() ЃЉЃЌAЃЈ
ЃЉЃЌAЃЈ ![]() ЃЌ3Љ
ЃЌ3Љ![]() ЃЉЃЎ
ЃЉЃЎ
гЩPЪЧABЕФжаЕуЃЌЕУ
PЃЈ ![]() ЃЌ3ЃЉ
ЃЌ3ЃЉ
ЕБx= ![]() ЪБЃЌy=2x2=
ЪБЃЌy=2x2= ![]() ЃЌМДCЕузјБъЮЊЃЈ
ЃЌМДCЕузјБъЮЊЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈbЃЉAB2=ЃЈ ![]() Љ
Љ ![]() ЃЉ2+ЃЈ3+
ЃЉ2+ЃЈ3+ ![]() Љ3+
Љ3+ ![]() ЃЉ2=25ЃЛ
ЃЉ2=25ЃЛ
BC2=ЃЈ ![]() Љ
Љ ![]() ЃЉ2+ЃЈ3+
ЃЉ2+ЃЈ3+ ![]() Љ
Љ ![]() ЃЉ2=
ЃЉ2= ![]() Љ5
Љ5 ![]() ЃЛ
ЃЛ
AC2=ЃЈ ![]() Љ
Љ ![]() ЃЉ2+ЃЈ3Љ
ЃЉ2+ЃЈ3Љ ![]() Љ
Љ ![]() ЃЉ2=
ЃЉ2= ![]() +5
+5 ![]() ЃЌ
ЃЌ
ЁпAC2+BC2=AB2 ЃЌ
ЁрЁЯACB=90Ёу
ЁрЁїABCЪЧжБНЧШ§НЧаЮЃЛ
ЃЈcЃЉШчЭМ
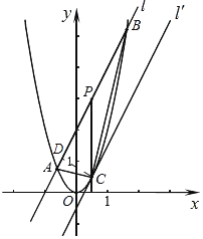
зїCDЁЭABгкDЕуЃЌCD ЪЧСНжБЯпМфЕФОрРыЃЌ
SЁїABC= ![]() ABCD=
ABCD= ![]() ACBCЃЌ
ACBCЃЌ
![]() ЁС5CD=
ЁС5CD= ![]() ЁС
ЁС ![]() ЃЌ
ЃЌ
НтЕУCD= ![]() ЃЎ
ЃЎ
СНжБЯпlгыlЁфЕФОрРыЪЧ ![]()


 ВНВНИпДяБъОэЯЕСаД№АИ
ВНВНИпДяБъОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
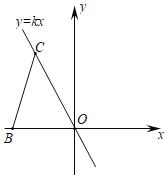
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпyЃНkxЃЈkЁй0ЃЉОЙ§ЕуЃЈmЃЌ![]() mЃЉЃЈmЃМ0ЃЉЃЎЯпЖЮBCЕФСНИіЖЫЕуЗжБ№дкxжсгыжБЯпyЃНkxЩЯЛЌЖЏЃЈBЁЂCОљгыдЕуOВЛжиКЯЃЉЃЌЧвBCЃН
mЃЉЃЈmЃМ0ЃЉЃЎЯпЖЮBCЕФСНИіЖЫЕуЗжБ№дкxжсгыжБЯпyЃНkxЩЯЛЌЖЏЃЈBЁЂCОљгыдЕуOВЛжиКЯЃЉЃЌЧвBCЃН![]() ЃЎЗжБ№зїBPЁЭxжсЃЌCPЁЭжБЯпyЃНkxЃЌжБЯпBPЁЂCPНЛгкЕуPЃЎОЬНОПЃЌдкећИіЛЌЖЏЙ§ГЬжаЃЌOЁЂPСНЕуМфЕФОрРыЮЊЖЈжЕЃЌдђИУОрРыЮЊ_____ЃЎ
ЃЎЗжБ№зїBPЁЭxжсЃЌCPЁЭжБЯпyЃНkxЃЌжБЯпBPЁЂCPНЛгкЕуPЃЎОЬНОПЃЌдкећИіЛЌЖЏЙ§ГЬжаЃЌOЁЂPСНЕуМфЕФОрРыЮЊЖЈжЕЃЌдђИУОрРыЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШєABЪЧЁбOЕФжБОЖЃЌCDЪЧЁбOЕФЯвЃЌЁЯABD=58ЁуЃЌдђЁЯBCD=________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБЪжБЕФЬњТЗЩЯAЁЂBСНЕуЯрОр25kmЃЌCЁЂDЮЊСНДхзЏЃЌDA=10kmЃЌCB=15kmЃЌDAЁЭABгкAЃЌCBЁЭABгкBЃЌЯжвЊдкABЩЯНЈвЛИіжазЊеОEЃЌЪЙЕУCЁЂDСНДхЕНEеОЕФОрРыЯрЕШЃЎЧѓEгІНЈдкОрAЖрдЖДІЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
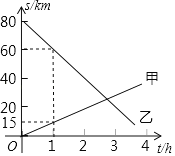
ЁОЬтФПЁПAЃЌBСНЕиЯрОр80kmЃЌМзЁЂввСНШЫЦяГЕЭЌЪБЗжБ№ДгAЃЌBСНЕиЯрЯђЖјааЃЌМйЩшЫћУЧЖМБЃГждШЫйааЪЛЃЌдђЫћУЧИїздЕНAЕиЕФОрРыs(km)ЖМЪЧЦяГЕЪБМфt(h)ЕФвЛДЮКЏЪ§ЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓввЕФsввгыtжЎМфЕФНтЮіЪНЃЛ
ЃЈ2ЃЉОЙ§ЖрГЄЪБМфМзввСНШЫЯрОр10kmЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЪЧГЃЪ§ЃЉЕФЭМЯѓОЙ§Еу
ЪЧГЃЪ§ЃЉЕФЭМЯѓОЙ§Еу![]() ЁЂЕу
ЁЂЕу![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЎЙ§Еу
ЃЎЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌДЙзуЮЊ
жсЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌДЙзуЮЊ
жсЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
(1)Шє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
(2)ЧѓжЄЃКЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЛ
ЮЊЦНааЫФБпаЮЃЛ
(3)Шє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФКЏЪ§НтЮіЪНЃЎ
ЕФКЏЪ§НтЮіЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌACЩЯЕФжаЯпBDАбШ§НЧаЮЕФжмГЄЗжЮЊ24ЉMКЭ30ЉMЕФСНИіВПЗжЃЌЧѓШ§НЧаЮЕФШ§БпГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈaЃЌbЃЉЕФзјБъТњзу|aЉb|+b2Љ8b+16ЃН0ЃЎ
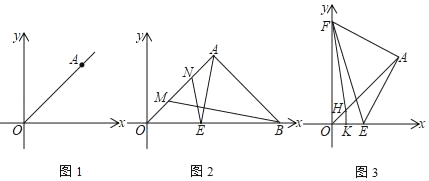
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКOAЪЧЕквЛЯѓЯоЕФНЧЦНЗжЯпЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§AзїOAЕФДЙЯпЃЌНЛxжсе§АыжсгкЕуBЃЌЕуMЁЂNЗжБ№ДгOЁЂAСНЕуЭЌЪБГіЗЂЃЌдкЯпЖЮOAЩЯвдЯрЭЌЕФЫйЖШЯрЯђдЫЖЏЃЈВЛАќРЈЕуOКЭЕуAЃЉЃЌЙ§AзїAEЁЭBMНЛxжсгкЕуEЃЌСЌBMЁЂNEЃЌВТЯыЁЯONEгыЁЯNEAжЎМфгаКЮШЗЖЈЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФВТЯыЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌFЪЧyжсе§АыжсЩЯвЛИіЖЏЕуЃЌСЌНгFAЃЌЙ§ЕуAзїAEЁЭAFНЛxжсе§АыжсгкЕуEЃЌСЌНгEFЃЌЙ§ЕуFЕузїЁЯOFEЕФНЧЦНЗжЯпНЛOAгкЕуHЃЌЙ§ЕуHзїHKЁЭxжсгкЕуKЃЌЧѓ2HK+EFЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
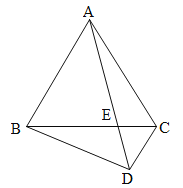
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABC ЪЧЕШБпШ§НЧаЮЃЌAB=4ЃЌE ЪЧBC БпЩЯШЮвтвЛЕу(ВЛгыBЁЂCжиКЯ)ЃЌдкШ§НЧаЮЭтзїЕШБпЁїCDEЃЌСЌНсAEЁЂBDЃЎ
(1)ИљОнЬтвтЛГіЭМаЮЃЛ
(2)ЧѓжЄЃКAE=BDЃЛ
(3)ЁїBDCФмЗёЮЊжБНЧШ§НЧаЮЃПШєФмЃЌЧѓГіBDГЄЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com