
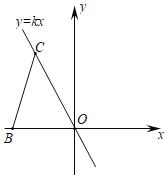
【题目】如图,在平面直角坐标系中,直线y=kx(k≠0)经过点(m,![]() m)(m<0).线段BC的两个端点分别在x轴与直线y=kx上滑动(B、C均与原点O不重合),且BC=
m)(m<0).线段BC的两个端点分别在x轴与直线y=kx上滑动(B、C均与原点O不重合),且BC=![]() .分别作BP⊥x轴,CP⊥直线y=kx,直线BP、CP交于点P.经探究,在整个滑动过程中,O、P两点间的距离为定值,则该距离为_____.
.分别作BP⊥x轴,CP⊥直线y=kx,直线BP、CP交于点P.经探究,在整个滑动过程中,O、P两点间的距离为定值,则该距离为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
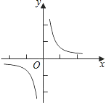
【题目】已知反比例函数![]() 的图象如图所示,点
的图象如图所示,点![]() ,
,![]() 是该图象上的两点.
是该图象上的两点.
(1)求![]() 的取值范围;
的取值范围;
(2)比较![]() 与
与![]() 的大小;
的大小;
(3)若点![]() 在该反比例函数图象上,求此反比例函数的解析式;
在该反比例函数图象上,求此反比例函数的解析式;
(4)若![]() 为第一象限上的一点,作
为第一象限上的一点,作![]() 轴于点
轴于点![]() ,求
,求![]() 的面积(用含
的面积(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .直线
.直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
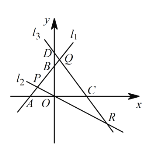
(1)点![]() 的坐标是 ,点
的坐标是 ,点![]() 的坐标是 ,点
的坐标是 ,点![]() 的坐标是 ;
的坐标是 ;
(2)将![]() 沿
沿![]() 轴折叠后,点
轴折叠后,点![]() 的对应点为
的对应点为![]() ,试判断点
,试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省济宁市)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )

A. 60B. 80C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
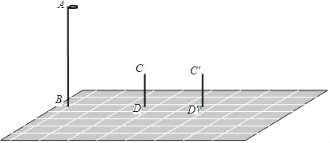
【题目】如图,AB表示路灯,CD、C′D′表示小明所在两个不同位置:
(1)分别画出这两个不同位置小明的影子;
(2)小明发现在这两个不同的位置上,他的影子长分别是自己身高的1倍和2倍,他又量得自己的身高为1.5米,DD′长为3米,你能帮他算出路灯的高度吗?(B、D、D′在一条直线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
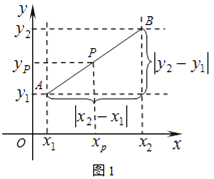
【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp﹣x1=x2﹣xp,得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为(![]() ,
,![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为________,MN=________.
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
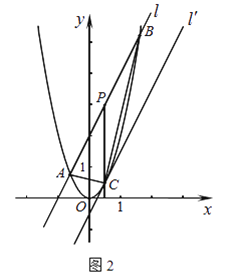
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com