
【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.
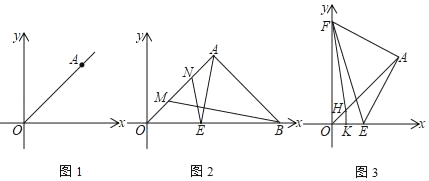
(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
【答案】(1)证明见解析 (2)答案见解析 (3)8
【解析】
(1)过点A分别作x轴,y轴的垂线,垂足分别为M、N,则AN=AM,
根据非负数的性质求出a、b的值即可得结论;
(2)如图2,过A作AH平分∠OAB,交BM于点H,则△AOE≌△BAH,可得AH=OE,由已知条件可知ON=AM,∠MOE=∠MAH,可得△ONE≌△AMH,∠ABH=∠OAE,设BM与NE交于K,则∠MKN=180°﹣2∠ONE=90°﹣∠NEA,即2∠ONE﹣∠NEA=90°;
(3)如图3,过H作HM⊥OF,HN⊥EF于M、N,可证△FMH≌△FNH,则FM=FN,同理:NE=EK,先得出OE+OF﹣EF=2HK,再由△APF≌△AQE得PF=EQ,即可得OE+OF=2OP=8,等量代换即可得2HK+EF的值.
解:(1)∵|a﹣b|+b2﹣8b+16=0
∴|a﹣b|+(b﹣4)2=0
∵|a﹣b|≥0,(b﹣4)2≥0
∴|a﹣b|=0,(b﹣4)2=0
∴a=b=4
过点A分别作x轴,y轴的垂线,垂足分别为M、N,则AN=AM
∴OA平分∠MON
即OA是第一象限的角平分线
(2)过A作AH平分∠OAB,交BM于点H
∴∠OAH=∠HAB=45°
∵BM⊥AE
∴∠ABH=∠OAE
在△AOE与△BAH中![]()
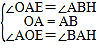 ,
,
∴△AOE≌△BAH(ASA)
∴AH=OE
在△ONE和△AMH中
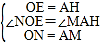 ,
,
∴△ONE≌△AMH(SAS)
∴∠AMH=∠ONE
设BM与NE交于K
∴∠MKN=180°﹣2∠ONE=90°﹣∠NEA
∴2∠ONE﹣∠NEA=90°
(3)过H作HM⊥OF,HN⊥EF于M、N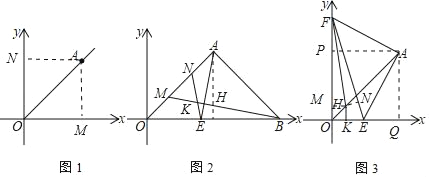
可证:△FMH≌△FNH(SAS)
∴FM=FN
同理:NE=EK
∴OE+OF﹣EF=2HK
过A作AP⊥y轴于P,AQ⊥x轴于Q
可证:△APF≌△AQE(SAS)
∴PF=EQ
∴OE+OF=2OP=8
∴2HK+EF=OE+OF=8


科目:初中数学 来源: 题型:
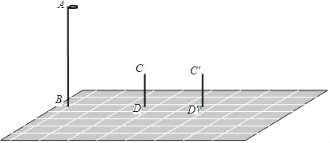
【题目】如图,AB表示路灯,CD、C′D′表示小明所在两个不同位置:
(1)分别画出这两个不同位置小明的影子;
(2)小明发现在这两个不同的位置上,他的影子长分别是自己身高的1倍和2倍,他又量得自己的身高为1.5米,DD′长为3米,你能帮他算出路灯的高度吗?(B、D、D′在一条直线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp﹣x1=x2﹣xp,得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为(![]() ,
,![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
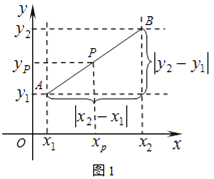
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为________,MN=________.
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
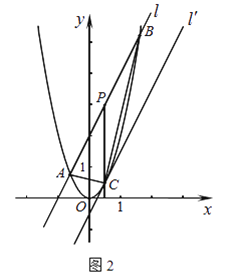
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的![]() 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
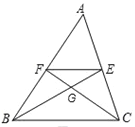
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE。

(1)试说明△BDE≌△CDF
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正六边形
的正六边形![]() ,在直线
,在直线![]() 上由图
上由图![]() 的位置按顺时针方向向右作无滑动滚动,当
的位置按顺时针方向向右作无滑动滚动,当![]() 第一次滚动到图
第一次滚动到图![]() 位置时,顶点
位置时,顶点![]() 所经过的路径的长为( )
所经过的路径的长为( )
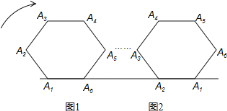
A. ![]() B. .
B. .![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
![]() 要使这两个正方形的面积之和等于
要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
![]() 小峰对小林说:“这两个正方形的面积之和不可能等于
小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“清明小假期”举行促销活动,设立了一个可以自由转动的转盘进行摇奖活动,并规定顾客每购买200元商品,就可以获得一次转动转盘的机会,小明根据活动情况绘制了一个扇形统计图,如图所示.
(1)求每转动一次转盘所获得购物券金额的平均数;
(2)小明做了一次实验,他转了200次转盘,总共获得5800元购物券,他平均每转动一次转盘获得的购物券是多少元?
(3)请你说明上述两个结果为什么有差别?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com