
【题目】小林准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
![]() 要使这两个正方形的面积之和等于
要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
![]() 小峰对小林说:“这两个正方形的面积之和不可能等于
小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
【答案】(1)较短的这段为16cm,较长的这段就为24cm;
(2)小峰的说法正确,这两个正方形的面积之和不可能等于44cm2.
【解析】
试题(1)利用正方形的性质表示出边长进而得出等式求出即可;
(2)利用正方形的性质表示出边长进而得出等式,进而利用根的判别式求出即可.
试题解析:设剪成的较短的这段为xcm,较长的这段就为(40﹣x)cm,
由题意,得(![]() )2+(
)2+(![]() )2=52;
)2=52;
解得:x1=16,x2=24,
当x=16时,较长的为40﹣16=24cm,当x=24时,较长的为40﹣24=16<24(舍去)
∴较短的这段为16cm,较长的这段就为24cm;
(2)设剪成的较短的这段为mcm,较长的这段就为(40﹣m)cm,
由题意得:(![]() )2+(
)2+(![]() )2=44,
)2=44,
变形为:m2﹣40m+448=0,
∵△=﹣192<0,∴原方程无解,
∴小峰的说法正确,这两个正方形的面积之和不可能等于44cm2.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.
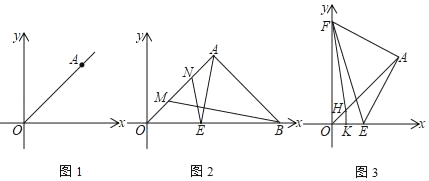
(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线![]() .
.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |

(3)利用以上信息解答下列问题:若关于x的一元二次方程![]() (t为实数)在
(t为实数)在![]() <x<
<x<![]() 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点.
(1)求证:GE是⊙O的切线;
(2)当△ADC满足怎样的条件时,四边形EGDO恰为正方形?(直接写出结果即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
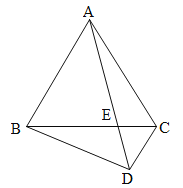
【题目】已知:如图,△ABC 是等边三角形,AB=4,E 是BC 边上任意一点(不与B、C重合),在三角形外作等边△CDE,连结AE、BD.
(1)根据题意画出图形;
(2)求证:AE=BD;
(3)△BDC能否为直角三角形?若能,求出BD长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹)
(2)连接DE,求证:△ADE≌△BDE。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com