
【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点.
(1)求证:GE是⊙O的切线;
(2)当△ADC满足怎样的条件时,四边形EGDO恰为正方形?(直接写出结果即可)

【答案】(1)见解析;(2)当△ADC满足∠A=45°时,四边形EGDO恰为正方形.
【解析】
(1)连接OE、DE,如图,利用圆周角定理得到∠CED=90°,再根据斜边上的中线性质得GE=GA=GD,则∠GED=∠GDE,加上∠OED=∠ODE,所以∠GEO=90°,然后根据切线的判定定理得到结论;
(2)当∠DOE=90°时易得四边形EGDO正方形,此时△OCE为等腰直角三角形,于是可判断当△ADC满足∠A=45°时,四边形EGDO恰为正方形.
(1)证明:连接OE、DE,如图,
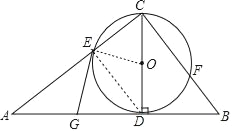
∵CD为直径,
∴∠CED=90°,
∵G点AD的中点,
∴GE=GA=GD,
∴∠GED=∠GDE,
而OD=OE,
∴∠OED=∠ODE,
∴∠GEO=∠GDC,
而CD为高,
∴∠GDC=90°,
∴∠GEO=90°,
∴OE⊥GE,
∴GE是⊙O的切线;
(2)当∠DOE=90°时,四边形EGDO为矩形,而OE=OD,则四边形EGDO正方形,
此时△OCE为等腰直角三角形,
所以当△ADC满足∠A=45°时,四边形EGDO恰为正方形.


科目:初中数学 来源: 题型:
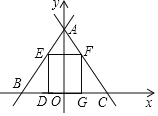
【题目】如图,直线y=kx+b与直线y=2x+6关于y轴对称且交于点A,直线y=2x+6交x轴于点B,直线y=kx+b交x轴于点C,正方形DEFG一边DG在线段BC上,点E在线段AB上,点F在线段AC上,则点G的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE。

(1)试说明△BDE≌△CDF
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程:![]() ,验证:
,验证:![]() .
.![]() , 验证:
, 验证:![]() .
.
(1)按照上述两个等式及其验证过程,猜想![]() 的变形结果并进行验证.
的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用a(a为任意自然数,且a≥2)表示的等式,并给出验证.
(3)针对三次根式及n次根式(n为任意自然数,且n≥2),有无上述类似的变形?如果有,写出用a(a为任意自然数,且a≥2)表示的等式,并给出验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
![]() 要使这两个正方形的面积之和等于
要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
![]() 小峰对小林说:“这两个正方形的面积之和不可能等于
小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
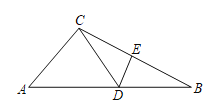
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE=2.
(1)若∠A=40°,求∠CDE;
(2)若图形中所有线段长均为整数,求CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
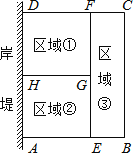
【题目】为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
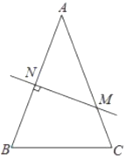
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)若![]() ,则
,则![]() 的度数是 ;
的度数是 ;
(2)连接![]() ,若
,若![]() ,
,![]() 的周长是
的周长是![]() .
.
①求![]() 的长;
的长;
②在直线![]() 上是否存在点
上是否存在点![]() ,使由
,使由![]() ,
,![]() ,
,![]() 构成的
构成的![]() 的周长值最小?若存在,标出点
的周长值最小?若存在,标出点![]() 的位置并求
的位置并求![]() 的周长最小值;若不存在,说明理由.
的周长最小值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com