
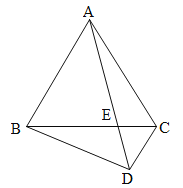
【题目】已知:如图,△ABC 是等边三角形,AB=4,E 是BC 边上任意一点(不与B、C重合),在三角形外作等边△CDE,连结AE、BD.
(1)根据题意画出图形;
(2)求证:AE=BD;
(3)△BDC能否为直角三角形?若能,求出BD长;若不能,请说明理由.
科目:初中数学 来源: 题型:
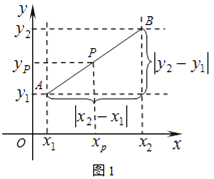
【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp﹣x1=x2﹣xp,得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为(![]() ,
,![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A、B两点间的距离公式为AB=![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为________,MN=________.
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
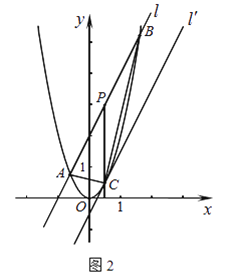
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
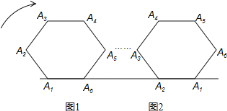
【题目】如图,将边长为![]() 的正六边形
的正六边形![]() ,在直线
,在直线![]() 上由图
上由图![]() 的位置按顺时针方向向右作无滑动滚动,当
的位置按顺时针方向向右作无滑动滚动,当![]() 第一次滚动到图
第一次滚动到图![]() 位置时,顶点
位置时,顶点![]() 所经过的路径的长为( )
所经过的路径的长为( )
A. ![]() B. .
B. .![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
![]() 要使这两个正方形的面积之和等于
要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
![]() 小峰对小林说:“这两个正方形的面积之和不可能等于
小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的长方形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
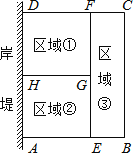
【题目】为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与![]() 轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O
轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O![]() A
A![]() C运动.
C运动.
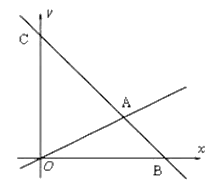
(1)求直线BC的解析式.
(2)求![]() 的面积.
的面积.
(3)当![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 时,求出这时点P的坐标.
时,求出这时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“清明小假期”举行促销活动,设立了一个可以自由转动的转盘进行摇奖活动,并规定顾客每购买200元商品,就可以获得一次转动转盘的机会,小明根据活动情况绘制了一个扇形统计图,如图所示.
(1)求每转动一次转盘所获得购物券金额的平均数;
(2)小明做了一次实验,他转了200次转盘,总共获得5800元购物券,他平均每转动一次转盘获得的购物券是多少元?
(3)请你说明上述两个结果为什么有差别?

查看答案和解析>>
科目:初中数学 来源: 题型:
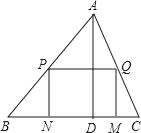
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com