
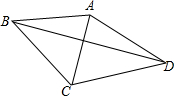
 ��ͼ���߶�AB=a�����߶�AB�Ƶ�A��ʱ����ת60��õ��߶�AC��������ת����0�㣼����120�㣩�õ��߶�AD������BC��CD��BD��
��ͼ���߶�AB=a�����߶�AB�Ƶ�A��ʱ����ת60��õ��߶�AC��������ת����0�㣼����120�㣩�õ��߶�AD������BC��CD��BD������ ��1���ɡ�BAD=90�㡢��BAC=60��ɵæ�����AC=AD�á�ADC=75�㡢��AB=AD�á�ADB=45�㣬�Ӷ��ó���BDC��BD�ij�����CE��AD�����CE���ٸ���S�ı���ABCD=S��ABC+S��ACD�ɵô𰸣�
��2����AC��AD��AC=AD=a�æ�=45�㡢CD=$\sqrt{2}$a����AB=AD=a����BAC=60��á�ABC=60�㡢��ADB=��ABD=15�㣬�Ӷ�֪��BDC=30�㡢��CBE=45�㣬��CE��BD����Rt��CDE��Rt��BCE�зֱ����DE��CE��BE�ij������ɵ�BD��������S�ı���ABCD=S��ABC+S��ACD�ɵô𰸣�
��3����AB=AC=AD=a֪��B��C��D���Ե�AΪԲ�ģ�aΪ�뾶��Բ�ϣ����ɵá�BDC=$\frac{1}{2}$��BAC=30�㣮
��� �⣺��1����AB��ADʱ����BAD=90�㣬����BAC+��CAD=90�㣬
�ߡ�BAC=60�㣬
���CAD=30�㣬����=30�㣬
��AC=AD��
���ADC=$\frac{180��-��CAD}{2}$=75�㣬
�֡�AB=AD=a����BAD=90�㣬
���ADB=45�㣬BD=$\sqrt{2}$a��
���BDC=��ADC-��ADB=30�㣬
��ͼ1����CE��AD�ڵ�E��
��CE=ACsin��CAE=$\frac{1}{2}$a��
��S�ı���ABCD=S��ABC+S��ACD=$\frac{\sqrt{3}}{4}$a2+$\frac{1}{2}$•a•$\frac{1}{2}$a=$\frac{\sqrt{3}+1}{4}$a2��
�ʴ�Ϊ��30��30��$\sqrt{2}$a��$\frac{\sqrt{3}+1}{4}$a2��
��2����ͼ2��
��AC��AD����AC=AD=a��
���ADC=45�㣬����=45�㣬CD=$\sqrt{2}$a��
�֡�AB=AD=a����BAC=60�㣬
���BAD=��BAC+��CAD=150�㣬��ABC=60�㣬
���ADB=��ABD=15�㣬
���BDC=��ADC-��ADB=30�㣬��CBE=��ABC-��ABD=45�㣬
��CE��BD�ڵ�E��
��Rt��CDE��DE=CDcos��BDC=$\sqrt{2}$a��$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{2}$a��
BE=CE=CDsin��BDC=$\sqrt{2}$a��$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$a��
��BD=DE+BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$a��
S�ı���ABCD=S��ABC+S��ACD=$\frac{\sqrt{3}}{4}$a2+$\frac{1}{2}$•a•a=$\frac{\sqrt{3}+2}{4}$a2��
�ʴ�Ϊ��90��30��$\frac{\sqrt{6}+\sqrt{2}}{2}$a��$\frac{\sqrt{3}+2}{4}$a2��
��3����BDC=$\frac{1}{2}$��BAC=30�㣬
��ͼ3��
��AB=AC=AD=a��
���B��C��D���Ե�AΪԲ�ģ�aΪ�뾶��Բ�ϣ�
�ߡ�BAC=60�㣬
���BDC=$\frac{1}{2}$��BAC=30�㣮
���� ������Ҫ������ת�����ʡ����������ε����ʡ�Բ�ܽǶ��������Ǻ�����Ӧ�ã��������ղ����������������ǽ���Ĺؼ���


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��Բ��������������ת����ת����������ɫ����Ϸ���ֱ�ת������ת�̣�������һ��ת����ɫ����һ��ת����ɫ���������ɫ����ô�������ɫ�ĸ����ǣ�������
��Բ��������������ת����ת����������ɫ����Ϸ���ֱ�ת������ת�̣�������һ��ת����ɫ����һ��ת����ɫ���������ɫ����ô�������ɫ�ĸ����ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{5}{12}$ | D�� | $\frac{7}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��
��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
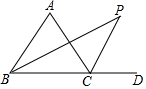 ��ͼ����ABC����ǡ�ACD��ƽ���ߣ�CP���ڽǡ�ABCƽ����BP���ڵ�P������A=60�㣬���P�Ķ�����
��ͼ����ABC����ǡ�ACD��ƽ���ߣ�CP���ڽǡ�ABCƽ����BP���ڵ�P������A=60�㣬���P�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
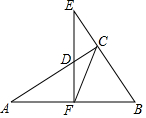 ��֪����ͼ����ABC�У���ACB=90�㣬FΪAB���е㣬EF��AB����֤����CDF�ס�ECF��
��֪����ͼ����ABC�У���ACB=90�㣬FΪAB���е㣬EF��AB����֤����CDF�ס�ECF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com