
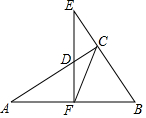
 已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB,求证:△CDF∽△ECF.
已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB,求证:△CDF∽△ECF.  仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
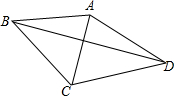 如图,线段AB=a,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接BC,CD,BD.
如图,线段AB=a,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接BC,CD,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,菱形OABC的顶点B在x轴上,其坐标为(6,0),菱形的面积为18$\sqrt{3}$
如图,在平面直角坐标系中,菱形OABC的顶点B在x轴上,其坐标为(6,0),菱形的面积为18$\sqrt{3}$查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:判断题
已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
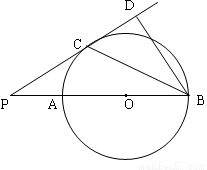
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com