
分析 根据题意可以画出相应的图形,可以得到存在两种情况,分别求出矩形的周长,本题得以解决.
解答 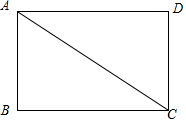 解:如右图所示,
解:如右图所示,
当∠ACB的余弦值为$\frac{1}{3}$时,
则cos∠ACB=$\frac{BC}{AC}=\frac{1}{3}$,
∵AC=9cm,
∴BC=3cm,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}=6\sqrt{2}$cm,
∴矩形的周长是:3+3+$6\sqrt{2}+6\sqrt{2}$=6+12$\sqrt{2}$;
当∠BAC的余弦值为$\frac{1}{3}$时,
则cos∠BAC=$\frac{AB}{AC}=\frac{1}{3}$,
∵AC=9cm,
∴AB=3cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}=6\sqrt{2}$cm,
∴矩形的周长是:3+3+$6\sqrt{2}+6\sqrt{2}$=6+12$\sqrt{2}$(cm);
由上可得,矩形的周长是:(6+12$\sqrt{2}$)cm,
故答案为:(6+12$\sqrt{2}$).
点评 本题考查解直角三角形、矩形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
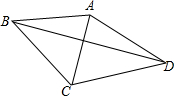 如图,线段AB=a,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接BC,CD,BD.
如图,线段AB=a,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接BC,CD,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com