
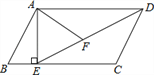
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
【答案】(1)证明见解析(2)6
【解析】试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
![]()
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴![]() ,∴DE=
,∴DE=![]() =
=![]() =12.
=12.
在Rt△ADE中,由勾股定理得:AE=![]() =
=![]() =6.
=6.


科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
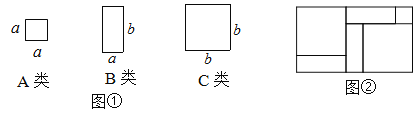

(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3) 如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上______ _____(填写序号)
①.xy =![]() ②.x+y=m ③.x2-y2=m·n ④.x2+y2 =
②.x+y=m ③.x2-y2=m·n ④.x2+y2 =![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.

(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有2位股东,20名工人、从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示.

(1)填写下表:
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 | 5000 | ||
股东的平均利润/元 | 25000 |
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com