
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

⑴20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
⑵与标准重量比较,20筐白菜总计超过或不足多少千克?
⑶若白菜每千克售价1.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(建立概念)如下图,A、B为数轴上不重合的两定点,点P也在该数轴上,我们比较线段![]() 和
和![]() 的长度,将较短线段的长度定义为点P到线段
的长度,将较短线段的长度定义为点P到线段![]() 的“靠近距离”.特别地,若线段
的“靠近距离”.特别地,若线段![]() 和
和![]() 的长度相等,则将线段
的长度相等,则将线段![]() 或
或![]() 的长度定义为点P到线段
的长度定义为点P到线段![]() 的“靠近距离”.
的“靠近距离”.
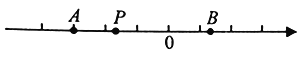
(概念理解)如下图,数轴的原点为O,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
(1)点O到线段![]() 的“靠近距离”为________;
的“靠近距离”为________;
(2)点P表示的数为m,若点P到线段![]() 的“靠近距离”为3,则m的值为_________;
的“靠近距离”为3,则m的值为_________;

(拓展应用)(3)如下图,在数轴上,点P表示的数为![]() ,点A表示的数为
,点A表示的数为![]() ,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为
,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为![]() 秒,当点P到线段
秒,当点P到线段![]() 的“靠近距离”为3时,求t的值.
的“靠近距离”为3时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.

(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
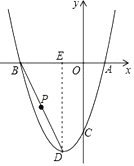
【题目】如图,已知抛物线y = x2 + bx + c的图象经过点A(l ,0) ,B(﹣3 ,0) ,与y轴交于点C ,抛物线的顶点为D ,对称轴与x轴相交于点E ,连接BD .
(1)求抛物线的解析式 .
(2)若点P在直线BD上,当PE = PC时,求点P的坐标 .
(3)在(2)的条件下,作PF⊥x轴于F ,点M为x轴上一动点 ,N为直线PF上一动点 ,G为抛物线上一动点,当以点F ,N ,G ,M 四点为顶点的四边形为正方形时,求点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OC⊥AB .在RtΔODE中,∠ODE=90°,∠DOE=30°,先将ΔODE一边OE与OC重合(如图1),然后将ΔODE绕点O按顺时针方向旋转(如图2),当OE与OC 重合时停止旋转.
(1)当∠AOD=80°时,则旋转角∠COE的大小为____________ ;
(2)当OD在OC与OB之间时,求∠AOD![]() ∠COE的值;
∠COE的值;
(3)在ΔODE的旋转过程中,若∠AOE=4∠COD时,求旋转角∠COE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点E在对角线AC上,连接BE、DE,
(1)如图1,作EM⊥AB交AB于点M,当AE=![]() 时,求BE的长;
时,求BE的长;
(2)如图2,作EG⊥BE交CD于点G,求证:BE=EG;
(3)如图3,作EF⊥BC交BC于点F,设BF=x,△BEF的面积为y.当x取何值时,y取得最大值,最大值是多少?当△BEF的面积取得最大值时,在直线EF取点P,连接BP、PC,使得∠BPC=45°,求EP的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com