
| A. | a≥8 | B. | a<8且a≠0 | C. | a≤8 | D. | a≤8且a≠0 |
分析 先由非负数的性质求出m与n的值,再根据关于x的一元二次方程ax2+mx+n=0有实数根及一元二次方程的定义,即可得判别式△≥0,a≠0,继而可求得a的范围.
解答 解:∵$\sqrt{m-8}$+|n-2|=0,
∴m-8=0,n-2=0,
∴m=8,n=2,
∵关于x的一元二次方程ax2+mx+n=0,即ax2+8x+2=0有实数根,
∴△=b2-4ac=82-4×a×2=64-8a≥0,
解得:a≤8,
∵方程ax2+8x+2=0是一元二次方程,
∴a≠0,
∴a的范围是:a≤8且a≠0.
故选D.
点评 此题考查了一元二次方程判别式的知识.此题比较简单,注意掌握一元二次方程有实数根,即可得△≥0.同时考查了非负数的性质与一元二次方程的定义.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| 古时 | 子时 | 丑时 | 寅时 | 卯时 |
| 今时 | 23:00~1:00 | 1:00~3:00 | 3:00~5:00 | 5:00~7:00 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
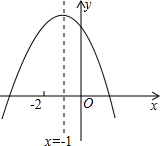 已知二次函数y=ax2+bx=c的图象如图,下列结论:
已知二次函数y=ax2+bx=c的图象如图,下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com