
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
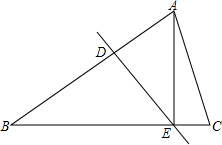 如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E
如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥8 | B. | a<8且a≠0 | C. | a≤8 | D. | a≤8且a≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
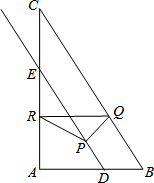 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D在AB上且AD=4,DE∥BC交AC于E,点P从点D出发沿射线DE运动,过点P作PQ⊥BC于Q,过点Q作QR∥AB交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,RQ=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D在AB上且AD=4,DE∥BC交AC于E,点P从点D出发沿射线DE运动,过点P作PQ⊥BC于Q,过点Q作QR∥AB交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,RQ=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
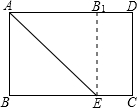 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为2cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com