
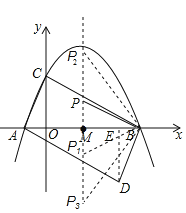
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
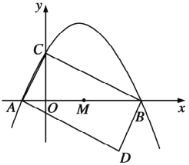
(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)将![]() 绕
绕![]() 的中点
的中点![]() 旋转
旋转![]() ,得到
,得到![]() .
.
①求点![]() 的坐标;
的坐标;
②判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在该抛物线对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似,若存在,请写出所有满足条件的
相似,若存在,请写出所有满足条件的![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 是直角三角形;(3)
是直角三角形;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)直接利用y=0,x=0分别得出A,B,C的坐标;
(2)①利用旋转的性质结合A,B,C的坐标得出D点坐标;
②利用勾股定理的逆定理判断![]() 的形状即可;
的形状即可;
(3)直接利用相似三角形的判定与性质结合三角形各边长进而得出答案.
解:(1)令![]() ,则
,则![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
令![]() ,则
,则![]() ,∴
,∴![]() ;
;
(2)①过![]() 作
作![]() 轴于点
轴于点![]() ,
,
∵![]() 绕点
绕点![]() 旋转
旋转![]() 得到
得到![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中
中
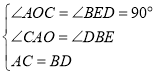 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() 在第四象限,
在第四象限,
∴![]() ;
;
②![]() 是直角三角形,
是直角三角形,
在![]() 中,
中,
![]() ,
,
在![]() 中
中
![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形;
是直角三角形;
(3)存在
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
作出抛物线的对称轴![]() ,
,
∵M是AB的中点,![]() ,
,![]() ,
,
∴M(![]() ,0),
,0),
∴点M在对称轴上.
∵点![]() 在对称轴上,
在对称轴上,
∴设![]() ,
,
当![]() 时,
时,
则![]() ,∴
,∴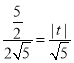 ,
,
![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
当![]() 时,
时,
则![]() ,∴
,∴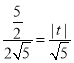 ,
,
![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
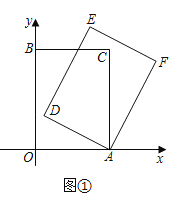
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
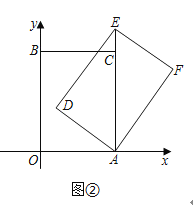
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;
(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,对称轴为直线x=1.以下结论:①2a>-b;②4a+2b+c>0;③m(am+b)>a+b(m是大于1的实数);④3a+c<0其中正确结论的个数为( )
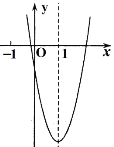
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化中心城区环境,政府计划在长为30米,宽为20米的矩形场地![]() 上修建公园.其中要留出宽度相等的三条小路,且两条与
上修建公园.其中要留出宽度相等的三条小路,且两条与![]() 平行,另一条与
平行,另一条与![]() 平行,其余部分建成花圃.
平行,其余部分建成花圃.
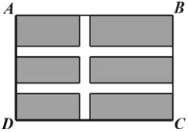
(1)若花圃总面积为448平方米,求小路宽为多少米?
(2)已知某园林公司修建小路的造价![]() (元)和修建花圃的造价
(元)和修建花圃的造价![]() (元)与修建面积
(元)与修建面积![]() (平方米)之间的函数关系分别为
(平方米)之间的函数关系分别为![]() 和
和![]() .若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一条抛物线,三位学生分别说出了它的一些性质:甲说:对称轴是直线![]() ;乙说:与
;乙说:与![]() 轴的两个交点的距离为6;丙说:顶点与
轴的两个交点的距离为6;丙说:顶点与![]() 轴的交点围成的三角形面积等于9,则这条抛物线解析式的顶点式是______.
轴的交点围成的三角形面积等于9,则这条抛物线解析式的顶点式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
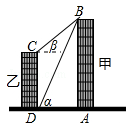
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() ,与
,与![]() 交于点
交于点![]() .
.
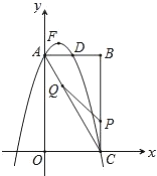
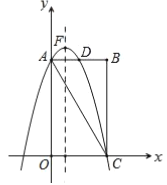
备用图
⑴求抛物线的函数解析式;
⑵点![]() 为线段
为线段![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),点
重合),点![]() 为线段
为线段![]() 上一个动点,
上一个动点,![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
⑶抛物线![]() 的顶点为
的顶点为![]() ,对称轴为直线
,对称轴为直线![]() ,当
,当![]() 最大时,在直线
最大时,在直线![]() 上,是否存在点
上,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,请写出符合条件的点
为顶点的四边形是平行四边形,若存在,请写出符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低3元,则平均每天的销售可增加30千克,若该专卖店销售这种核桃要想平均每天获利2090元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
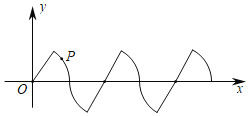
【题目】如图所示,在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是_____.
个单位长度,则第2018秒时,点P的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com