
【题目】如图,为美化中心城区环境,政府计划在长为30米,宽为20米的矩形场地![]() 上修建公园.其中要留出宽度相等的三条小路,且两条与
上修建公园.其中要留出宽度相等的三条小路,且两条与![]() 平行,另一条与
平行,另一条与![]() 平行,其余部分建成花圃.
平行,其余部分建成花圃.
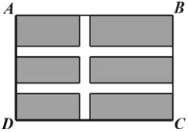
(1)若花圃总面积为448平方米,求小路宽为多少米?
(2)已知某园林公司修建小路的造价![]() (元)和修建花圃的造价
(元)和修建花圃的造价![]() (元)与修建面积
(元)与修建面积![]() (平方米)之间的函数关系分别为
(平方米)之间的函数关系分别为![]() 和
和![]() .若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
【答案】(1)小路的宽为2米;(2)小路的宽为2米时修建小路和花圃的总造价最低.
【解析】
(1)设小路的宽为![]() 米,根据面积公式列出方程并解方程即可;
米,根据面积公式列出方程并解方程即可;
(2)设小路的宽为![]() 米,总造价为
米,总造价为![]() 元,先分别表示出花圃的面积和小路的面积,然后根据已知函数关系,即可求出总造价为
元,先分别表示出花圃的面积和小路的面积,然后根据已知函数关系,即可求出总造价为![]() 与小路宽
与小路宽![]() 的函数关系式,化为顶点式,利用二次函数的增减性求最值即可求出此时的小路的宽.
的函数关系式,化为顶点式,利用二次函数的增减性求最值即可求出此时的小路的宽.
解:(1)设小路的宽为![]() 米,则可列方程
米,则可列方程
![]()
解得:![]() 或
或![]() (舍去)
(舍去)
答:小路的宽为2米.
(2)设小路的宽为![]() 米,总造价为
米,总造价为![]() 元,
元,
则花圃的面积为![]() 平方米,小路面积为
平方米,小路面积为![]() =
=![]() 平方米
平方米
所以![]()
整理得:![]()
∵![]() ,对称轴为x=20
,对称轴为x=20
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
∴当![]() 时,
时,![]() 取最小值
取最小值
答:小路的宽为2米时修建小路和花圃的总造价最低


科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
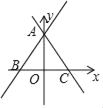
【题目】如图,直线y=![]() x+
x+![]() 与x轴相交于点B,与y轴相交于点A.
与x轴相交于点B,与y轴相交于点A.
(1)求∠ABO的度数;
(2)过点A的直线l交x轴的正半轴于点C,且AB=AC,求直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
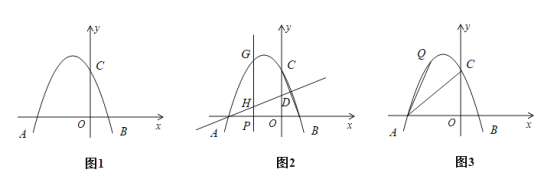
(1)求抛物线的解析式.
(2)如图2,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 点是
点是![]() 轴上一个动点,过点
轴上一个动点,过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,当点
,当点![]() 、
、![]() 、
、![]() 、
、![]() 四个点组成的四边形是平行四边形时,求此时
四个点组成的四边形是平行四边形时,求此时![]() 点坐标.
点坐标.
(3)如图3,连接![]() 和
和![]() ,
,![]() 点是抛物线上一个动点,连接
点是抛物线上一个动点,连接![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
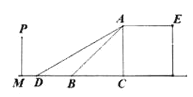
【题目】某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求舞台的高AC(结果保留根号)
(2)楼梯口B左侧正前方距离舞台底部C点3m处的文化墙PM是否要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
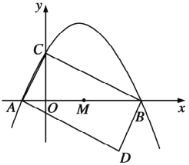
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)将![]() 绕
绕![]() 的中点
的中点![]() 旋转
旋转![]() ,得到
,得到![]() .
.
①求点![]() 的坐标;
的坐标;
②判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在该抛物线对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似,若存在,请写出所有满足条件的
相似,若存在,请写出所有满足条件的![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
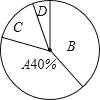
【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 45~50 | 40 | 0.4 |
B | 40~44 | 42 | x |
C | 35~39 | m | 0.12 |
D | 30~34 | 6 | 0.03 |
合计 | 1.00 |
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.
查看答案和解析>>
科目:初中数学 来源: 题型:
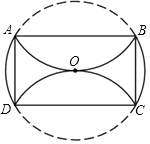
【题目】如图,在⊙O中,分别将![]() 、
、![]() 沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
A.8B.![]() C.32D.
C.32D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com