
【题目】如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中 ![]() =1.732)
=1.732)
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD//BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB,OA交⊙O于点E. 
(1)证明:直线AB与⊙O相切;
(2)若AE=a,AB=b,求⊙O的半径;(结果用a,b表示)
(3)过点C作弦CD⊥OA于点H,试探究⊙O的直径与OH、OB之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.
(1)去年的批发价和今年网上售价分别是多少?
(2)若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: ①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正确的结论的个数是 . 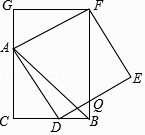
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com