
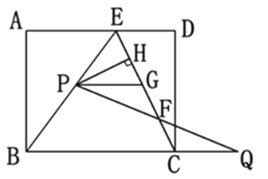
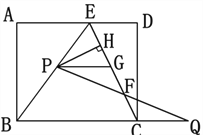
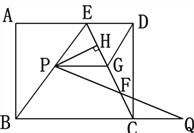
【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由;
(3)作PH⊥EC于点H.探究:
①点P在运动过程中,线段HF的长度是否发生变化?若变化,说明理由;若不变,求HF的长度;
②当x为何值时,△PHF与△BAE相似
【答案】(1)证明见解析;(2)当x=4时,四边形PGDE是菱形,理由见解析;(3)①不变化,HF![]() ,②当
,②当![]() 或
或![]() 时,△PHF与△BAE相似
时,△PHF与△BAE相似
【解析】试题分析:(1)根据全等三角形的判定ASA即可证出;(2)先证出PG∥BQ,AD∥BC得到四边形PGDE是平行四边形,再根据四边形PGDE是菱形得出PG=PE=4;(3)① 证出△PFG≌△QFC,求出HF的长;②分两种情况讨论得出.
试题解析:
(1)证明:∵BC=BE ∴∠BCE=∠PEC
∵PG∥BQ
∴∠BCE=∠PGE, ∠Q=∠FPG ,∠QCF=∠PGF
∴∠PGE=∠PEC
∴PE=PG
∵PE=CQ
∴ PG =CQ
∴△PFG≌△QFC (ASA)
(2)连结DG.当x=4时,四边形PGDE是菱形,
理由如下;
∵四边形ABCD是矩形,
∴AD∥BC
AB=CD=8,AD=BC=BE=10
在Rt△ABE中
AE=![]()
∴DE=AD-AE=10-6=4
由(1)知PG=PE=x=4
∴PG=DE
∵PG∥BQ,AD∥BC
∴PG∥DE
∴四边形PGDE是平行四边形,
∵PG=PE=4
∴四边形PGDE是菱形
(3)①不变化
在Rt△ABE中
CE=![]()
∵PG=PE,PH⊥EC
∴EH=HG=![]() EG(等腰三角形“三线合一”)
EG(等腰三角形“三线合一”)
∵△PFG≌△QFC
∴CF=GF=![]() CG
CG
∴HF=HG+FG=![]() EG+
EG+![]() CG=
CG=![]() CE=
CE=![]()
②∵PG∥DE, ∴∠DEC=∠PGH
在Rt△PGH中
PH=PG×sin∠PGH= x×sin∠DEC= x×![]() = x×
= x×![]() =
=![]()
分两种情况讨论:
(I)若△PHF∽△EAB,则![]()
∴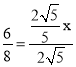
∴![]()
∴当![]() 时,△PHF∽△BAE.
时,△PHF∽△BAE.
(II)若△PHF∽△BAE,则![]()
∴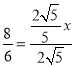
∴![]()
∴当![]() 或
或![]() 时,△PHF与△BAE相似
时,△PHF与△BAE相似


科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”对函数y=x2-2|x|+1的图象和性质进行了探究,探究过程
如下,请补充完整.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | 4 | 1 | 0 | 1 | 0 | 1 | 4 | … |
(1)由于自变量x的取值范围是全体实数,则可列得下表.根据表中数据,在如图所示
的平面直角坐标系中画出该函数的图象.

(2)观察函数图象,写出两条函数的性质:
①_______________________________________;
②_______________________________________.
(3)进一步探究函数图象发现:
①函数y=x2-2|x|+1,当 x=__时,y取最小值,
最小值为__;
②因为函数图象与x轴有两个交点,所以y=0,
即方程x2-2|x|+1=0有_________个不相等的实数根;
③方程x2-2|x|+1=1有_______个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
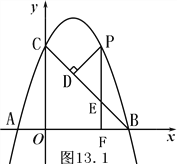
【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<3),过点P作PD⊥BC于点D. ① 求线段PD的长的最大值;② 当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1)、B(-4,-3)、C(-4,-1).
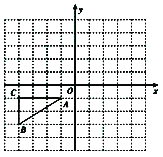
(1)作出△ABC关于原点O中心对称的图形△A′B′C′;
(2)将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1,画出△A1B1C1,并写出点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com