
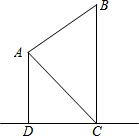
 在一次数学课外活动中,一位同学在教学楼的点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,旗杆底部C的俯角为45°.已知A点距地面的高度为20m,求旗杆的高度.
在一次数学课外活动中,一位同学在教学楼的点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,旗杆底部C的俯角为45°.已知A点距地面的高度为20m,求旗杆的高度. 分析 过A作AE⊥BC于E,在Rt△ACE中,已知了CE的长,可利用俯角∠CAE的正切函数求出AE的值;进而在Rt△ABE中,利用仰角∠BAE的正切函数求出BE的长,最后根据BC=BE+CE即可求解
解答 解:过A作AE⊥BC于E.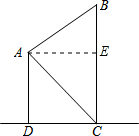
∵AD∥CE,
∴Rt△ACE中,CE=AD=20m,∠CAE=45°,
∴AE=CE÷tan45°=20(m).
Rt△AEB中,
∵AE=20m,∠BAE=30°,
∴BE=AE•tan30°=$\frac{20\sqrt{3}}{3}$(m).
BC=BE+CE=20+$\frac{20\sqrt{3}}{3}$(m).
故旗杆的高度为(20+$\frac{20\sqrt{3}}{3}$)m.
点评 本题考查直角三角形的应用,首先构造直角三角形,再运用三角函数的定义解题,是中考常见题型,解题的关键是作出垂线构造直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播放新闻 | |
| B. | 调查炮弹的发射距离远近情况适合普查 | |
| C. | 给定一组数据,那么这组数据的中位数一定只有一个 | |
| D. | 盒子里装有三个红球和三个黑球,搅匀后从中摸出两球,一定一红一黑 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两边相等的平行四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 四个角相等的菱形是正方形 | D. | 两条对角线相等的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
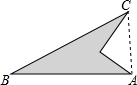 一个零件的形状如图所示,按规定∠BAC应为直角,工人师傅测得∠ADC=90°,AD=6,CD=8,AB=24,BC=26,请你帮他看一下,这个零件符合要求吗?为什么.
一个零件的形状如图所示,按规定∠BAC应为直角,工人师傅测得∠ADC=90°,AD=6,CD=8,AB=24,BC=26,请你帮他看一下,这个零件符合要求吗?为什么.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com