
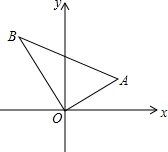
 如图所示,Rt△ABO的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A、B两点坐标和△ABO的面积.
如图所示,Rt△ABO的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A、B两点坐标和△ABO的面积. 分析 根据已知和勾股定理求出OB,根据三角形的面积公式求出△ABO的面积,作AC⊥x轴于C,BD⊥x轴于D,根据直角三角形的性质求出AC、OC得到点A的坐标,求出OB、OD得到点B的坐标.
解答 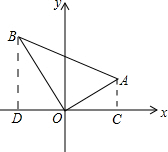 解:作AC⊥x轴于C,BD⊥x轴于D,
解:作AC⊥x轴于C,BD⊥x轴于D,
在Rt△ABO中,OA=6,AB=10,
由勾股定理得,OB=8,
∴△ABO的面积为:$\frac{1}{2}$×OA×OB=24;
∵OA=6,∠AOC=30°,
∴AC=$\frac{1}{2}$OA=3,OC=3$\sqrt{3}$,
∴点A的坐标为(3$\sqrt{3}$,3),
∵∠AOB=90°,∠AOC=30°,
∴∠OBD=30°,OB=8,
∴OD=4,BD=4$\sqrt{3}$,
∴点B的坐标为(4,4$\sqrt{3}$).
点评 本题考查的是解直角三角形和坐标与图形性质,掌握锐角三角函数的概念和勾股定理是解题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:填空题
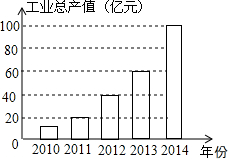 如图是根据某市2010年至2014年的工业生产总值绘制的条形统计图,观察统计图可以看出,工业生产总值(亿元)增长最多的年份是2014年.
如图是根据某市2010年至2014年的工业生产总值绘制的条形统计图,观察统计图可以看出,工业生产总值(亿元)增长最多的年份是2014年.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
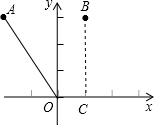 对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小长度为G1、G2的“密距”.例如,如上图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3.如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k值为( )
对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小长度为G1、G2的“密距”.例如,如上图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3.如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k值为( )| A. | k=4 | B. | k=-4 | C. | k=6 | D. | k=-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 中位数 | D. | 众数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com