
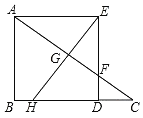
【题目】如图,在Rt△ABC中,∠B=90°,BC>AB,在BC边上取点D,使AB=BD,构造正方形ABDE,DE交AC于点F,作EG⊥AC交AC于点G,交BC于点H.
(1)求证:EF=DH;
(2)若AB=6,DH=2DF,求AC的长.
【答案】(1)见解析;(2)3![]()
【解析】
(1)根据正方形的性质及同角的余角相等建立AAS即可证明△AFE≌△EHD,再根据全等三角形的性质即可得出答案;
(2)设DF=x,则EF=DH=2x,根据AB=6即可求出x的值;再证明△AEF∽△CDF即可求出BC的值,最后根据勾股定理即可得出答案.
解:(1)证明:在正方形ABDE中,AE=ED,∠AEF=∠EDH=90°
∴∠DHE+∠GEF=90°
∵EG⊥AC
∴∠GEF+∠GFE=90°
∴∠GFE=∠DHE
在△AFE和△EHD中
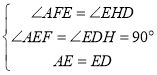
∴△AFE≌△EHD(AAS)
∴EF=DH;
(2)∵DH=2DF,EF=DH
∴设DF=x,则EF=DH=2x
∵AB=6
∴AE=DE=6
∴x+2x=6
∴x=2
∴DF=2,EF=4
∵在正方形ABDE中,AE∥BD
∴△AEF∽△CDF
∴![]()
∴![]()
∴DC=3
∴BC=BD+DC=6+3=9
∴在Rt△ABC中,由勾股定理得:
AC=![]() =
=![]() =
=![]()
∴AC的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:对角线互相垂直的四边形叫做垂美四边形.

(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;
(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.
①求证:四边形BCGE是垂美四边形;
②若AC=4,AB=5,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网购已经成为一种时尚,某网络购物平台“双十一”全天交易额逐年增长,2016年交易额为500亿元,2018年交易额为720亿元。
(1)2016年至2018年“双十一”交易额的年平均增长率是多少?
(2)若保持原来的增长率,试计算2019年该平台“双十一”的交易额将达到多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
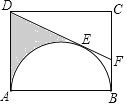
【题目】矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=![]() ,则阴影部分的面积为_____.
,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
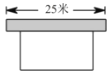
【题目】如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的长、宽各为多少米,设与墙平行的一边长为![]() 米.
米.
(1)填空:(用含![]() 的代数式表示)另一边长为 米;
的代数式表示)另一边长为 米;
(2)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
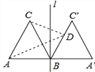
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.

(问题解决)
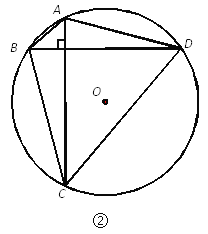
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com