
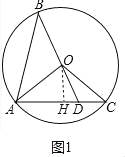
【题目】如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离;
(3)记△AOB、△AOD、△COD 的面积分别为S1、S2、S3,如果S2是S1和S3的比例中项,求OD的长.
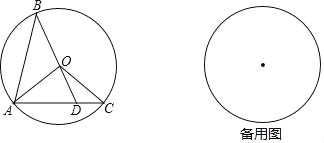
【答案】(1)证明见解析;(2)BC=![]() .(3)OD=
.(3)OD=![]() .
.
【解析】
试题分析:(1)由△AOB≌△AOC,推出∠C=∠B,由OA=OC,推出∠OAC=∠C=∠B,由∠ADO=∠ADB,即可证明△OAD∽△ABD;
(2)如图2中,当△OCD是直角三角形时,可以证明△ABC是等边三角形即可解决问题;
(3)如图3中,作OH⊥AC于H,设OD=x.想办法用x表示AD、AB、CD,再证明AD2=ACCD,列出方程即可解决问题;
试题解析:(1)如图1中,
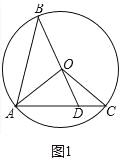
在△AOB和△AOC中,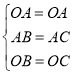 ,∴△AOB≌△AOC,∴∠C=∠B,
,∴△AOB≌△AOC,∴∠C=∠B,
∵OA=OC,∴∠OAC=∠C=∠B,∵∠ADO=∠ADB,∴△OAD∽△ABD.
(2)如图2中,
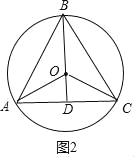
∵BD⊥AC,OA=OC,∴AD=DC,∴BA=BC=AC,∴△ABC是等边三角形,
在Rt△OAD中,∵OA=1,∠OAD=30°,∴OD=![]() OA=
OA=![]() ,∴AD=
,∴AD=![]() =
=![]() ,∴BC=AC=2AD=
,∴BC=AC=2AD=![]() .
.
(3)如图3中,作OH⊥AC于H,设OD=x.
∵△DAO∽△DBA,∴![]() ,∴
,∴![]() ,∴AD=
,∴AD=![]() ,AB=
,AB=![]() ,
,
∵S2是S1和S3的比例中项,∴S22=S1S3,
∵S2=![]() ADOH,S1=S△OAC=
ADOH,S1=S△OAC=![]() AC﹒OH,S3=
AC﹒OH,S3=![]() CD﹒OH,∴(
CD﹒OH,∴(![]() AD﹒OH)2=
AD﹒OH)2=![]() AC﹒OH﹒
AC﹒OH﹒![]() CD﹒OH,
CD﹒OH,
∴AD2=ACCD,
∵AC=AB.CD=AC﹣AD=![]() ﹣
﹣![]() ,
,
∴(![]() )2=
)2=![]() (
(![]() ﹣
﹣![]() ),
),
整理得x2+x﹣1=0,
解得x=![]() 或
或![]() ,
,
经检验:x=![]() 是分式方程的根,且符合题意,
是分式方程的根,且符合题意,
∴OD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). 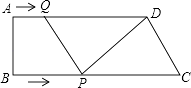
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C、D、Q、P为顶点的梯形面积等于60cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:
解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a= , b= .
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com